Um determinado sistema tem sua capacidade variando com um parâmetro através de dois modelos definidos dependentes do valor de . Quando é não-negativo sabe-se que , e quando é negativo sabe-se que . Você é o engenheiro responsável e precisa entender o total funcionamento do sistema com a variação do parâmetro . Com isso:
- Faça o esboço do modelo completo da capacidade do sistema para a variação de em todo . (Obs.: Devem ser apresentados todos os cálculos antes do desenho do esboço, englobando todos os passos vistos em teoria em sala).
- Os pontos críticos obtidos na capacidade do sistema quando varia em todo .
- Os pontos de inflexão obtidos na capacidade do sistema quando varia em todo .
- Sabendo que o sistema funcionará apenas para e , determine, caso existam, os máximos e mínimos globais para cada um dos intervalos de funcionamento.
Passo 1
Fala, galerinha! Construção de gráficos é uma tarefa metódica, devemos ter uma cadeia de passos a qual sempre seguiremos que nos forneça informações relevantes. Seguindo o passo a passo da questão podemos chegar no desenho correto, acompanha:
DESCONTINUIDADES: Observe que se aproximando de a função diverge pela esquerda e converge pela direita. E a derivada para e não deve existir, apesar da função ser definida nesses pontos indicando bicos no gráfico.
PRIMEIRA DERIVADA: para
PONTOS CRÍTICOS: ou
Em a derivada diverge pela esquerda e converge pela direita, logo . Veja ainda que para , , para . Se a derivada se anula para :
E se esta se anula para :
Logo, para a derivada se anula e para a derivada não existe. Tendo
Donde em a função é descontínua e nos outros dois pontos nos quais previa-se um bico na função, teremos inclinações de , isto é, , verticais. Em , a função há de subir na vertical e depois descer, enquanto em a função tratará de subir na vertical apenas.
São os pontos críticos:
CRESCIMENTO: Fazendo o estudo de sinal, usando como pontos de referência os obtidos acima, teremos:
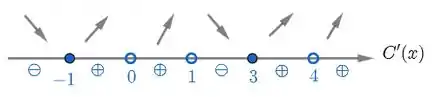
Assim, os extremos do domínio são (máximo local), e (mínimos locais), uma vez que o crescimento se inverte nestes pontos.
Passo 2
Derivando a expressão da primeira derivada:
SEGUNDA DERIVADA: para , temos:
PONTOS DE INFLEXÃO:
Repare que não há pontos de inflexão para , contudo para , se a segunda derivada se anula:
Logo, representa os pontos de inflexão nos quais há mudança de concavidade.
CONCAVIDADE: determinada pelo sinal de ,usaremos como pontos de referência do estudo de sinal os pontos de inflexão e as descontinuidades :
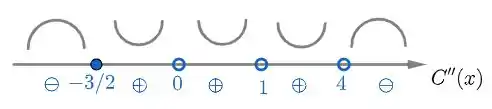
Repare, todavia, que a concavidade muda em e a função é contínua neste ponto, logo mesmo que a segunda derivada não seja nula em , este é um ponto de inflexão.
Passo 3
ASSÍNTOTAS VERTICAIS: geralmente, ocorrem em descontinuidades. Basta verificar em , portanto. Observe que para:
Teremos
Logo, temos uma assíntota vertical pela direita: , com .
ASSÍNTOTAS NÃO-VERTICAIS:essas ocorrem em quando a função tende a . O passo a passo é verificar se é finito, para depois verificar se é finito. Assim, observe que:
Agora,
Aqui usaremos o truque de multiplicar :
Logo, para , é assíntota. E ainda,
Agora,
Logo, para , também é assíntota.
Passo 4
PONTOS DE REFERÊNCIA: Para fazer o esboço é bom tomar alguns pontos de referência como os pontos de inflexão e os críticos. Anotando seus valores no gráfico.
ESBOÇO:
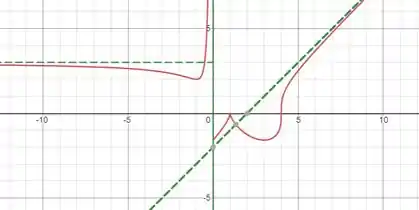
Passo 5
Analisando o intervalo , onde , o mínimo local obviamente será global, uma vez que comparado aos outros candidatos (extremidades do intervalo) é o menor:
E o máximo global ocorre em , pois apresenta valor maior que a outra extremidade que apenas tende a 3 inferiormente.
Enquanto isso, o intervalo apresenta um máximo local em e um mínimo local em , sabendo que os candidatos (extremos locais e extremidades do intervalo) são tais que
Temos que é máximo global, visto que é maior que os outros candidatos a máximo. Enquanto, ambas as extremidades são pontos de mínimo global, visto que são menores que os outros candidatos.
Resposta
-
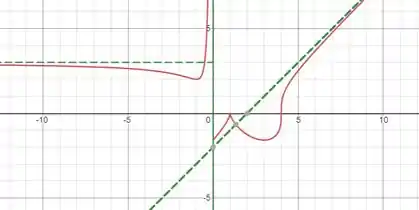
- : Mín: Máx:
: Mín: Máx: