Encontre as assíntotas verticais e horizontais da seguinte função
Depois faça um esboço do gráfico de .
Passo 1
Antes de qualquer coisa vou analisar os dois termos (numerador e denominador) de e tentar abrir em um produto de polinômios irredutíveis.
Podemos simplificar , dessa forma:
Podemos simplificar aquele , mas é importante lembrar aqui o domínio da função.
Ele pediu o gráfico no fim da questão, mas estamos dando uma manipulada na expressão da função, nessas horas é importante ficarmos atentos ao domínio da função.
Isso porque as vezes nós cortamos coisas e esquecemos delas no final.
Aqui não podemos ter denominadores negativos, então
Assim, o domínio vai ser qualquer número diferente de e
Passo 2
Vamos voltar para a nossa função
Agora vamos cortar aquele
Ok, vamos procurar as assíntotas agora.
Passo 3
Seguinte, Assíntotas verticais aparecem onde o domínio não está definido e as horizontais aparecem quando usamos o limite em .
Começando com as verticais, o domínio não está definido em
Asíntota vertical em .
Passo 4
Vamos usar o limite de em e em
Achamos uma mesma assíntota horizontal, .
Passo 5
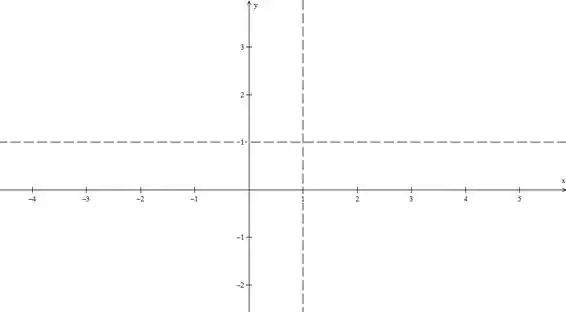
Agora, temos que usar isso para fazer um esboço do gráfico. Vou juntar os limites
Vamos traçar as assíntotas no plano cartesiano primeiro, colocando retas pontilhadas
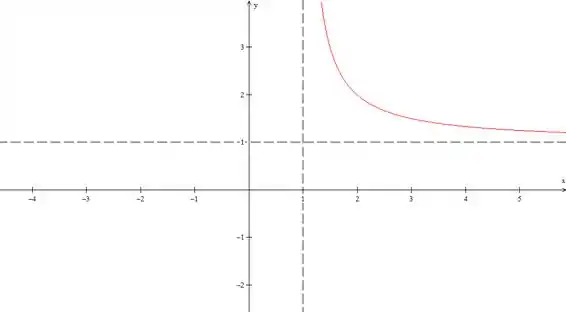
Pelos limites, vamos ver que a nossa função logo depois de , ou seja, com , vai vir de e depois vai ser assintótica com . Vamos desenhar isso
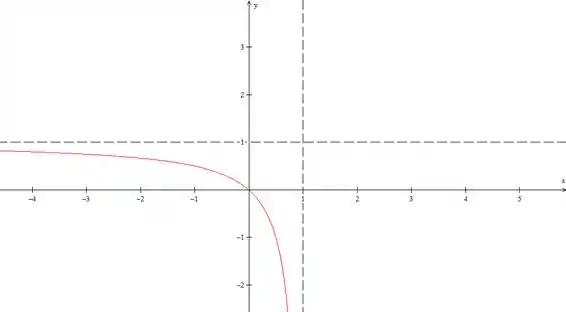
Agora falta a outra parte, a função vem próxima de , e vai se afastando para valores cada vez menores indo até o quando , o gráfico dessa parte vai ser
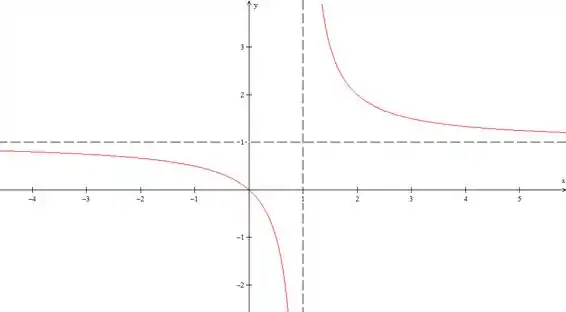
O nosso gráfico vai ser alto mais ou menos assim
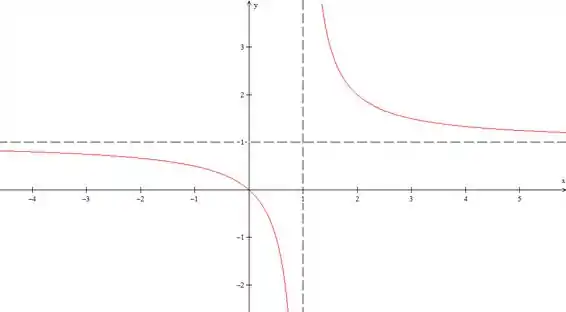
Resposta
Assíntota vertical:
Assíntota horizontal: