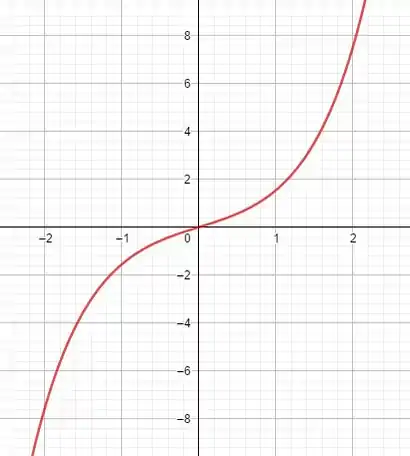
Encontre, se existirem, as assíntotas horizontais e verticais do gráfico da função e esboce o seu gráfico.
Passo 1
Reescrever a função
Trabalhar na forma de função hiperbólica nem sempre é o mais fácil. Nesse caso, como queremos ver assíntotas, vamos lembrar que:
E reescrever a função do enunciado como:
Essa expressão aí vai ser mais fácil de trabalhar. Então bora começar achando as assíntotas do gráfico!
Passo 2
Achar as assíntotas verticais
Pra achar as assíntotas verticais, o que a gente precisa fazer é olhar no fundo dos olhos da função e perguntar: eai, você tem algum que gere uma indefinição? Em uma função que é soma de quocientes, a única indefinição possível é:
E veja que, no nosso caso:
Se eu posso dar qualquer pra função e receber um como resposta, então não tem nenhuma assíntota vertical!
Passo 3
Achar as assíntotas horizontais
Agora que a gente começa a por a mão na massa e fazer conta. Pra achar assíntotas verticais a gente tem que olhar de novo no fundo dos olhos da função, mas dessa vez perguntar: existe algum que você nunca alcance valor igual ou maior? Ou que tal igual ou menor?
Em matematiquês, essa pergunta é o mesmo que calcular:
Então vamo que vamo:
Dividimos então o limite em dois e o segundo, acabamos ficando com uma indeterminação que tem a cara de L’Hospital. Derivando em cima e em baixo então, ficamos com:
Beleza, agora é só aplicar os limites. Vamos ter:
Eta, infinito não é um número! Então já podemos logo afirmar que não existe assíntotal horizontal do lado direito do eixo , isto é, para . Agora, para , vamos ter que:
Só um detalhe quando trabalhamos com qualquer coisa elevada a : já que estamos tendendo a , valores cada vez maiores em módulo porém negativos farão com que possamos considerar
Então do primeiro limite, podemos fazer:
E aplicando L’Hospital:
Pro segundo limite vamos ter::
E de novo, se infinito não é um número, menos infinito também não é! Então podemos afirmar também que não existe assíntotal horizontal do lado esquerdo do eixo . Ou seja, a malandra da função não tem assíntota nenhuma.
Passo 4
Esboçar o gráfico
Olha só que maneiro que a gente achou:
O que esse resultado nos diz é que a função é crescente o tempo todo! Show de bola, mas será que passa na horigem? Vamos ver:
Opa, passa na origem sim! Então já sabemos que vai ser algo no estilo de
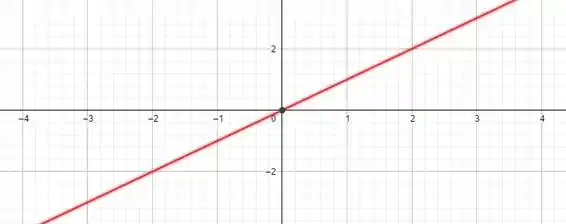
Mas claro, essa função vai ter umas curvinhas! Cortesia do produto . Como a gente só quer um esboço, vamos tentar ir substituindo uns pontos ao entorno de :
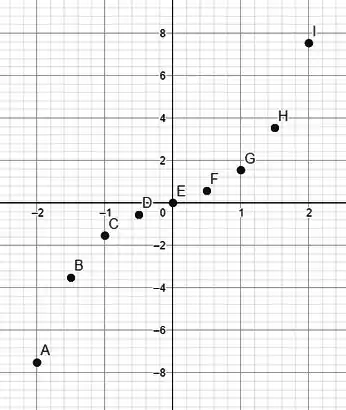
Ligando os pontos:
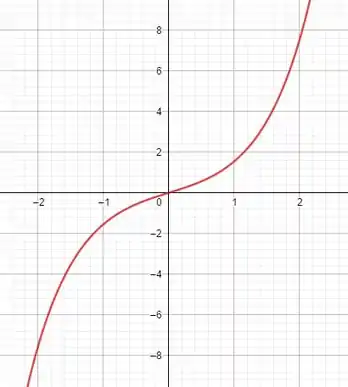
Resposta
A função não possui assíntotas.