UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 7.3
Esboce o gráfico de
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar o gráfico da seguinte função:
Mas como podemos esboçar essa função???
Uma forma seria escolher valores aleatórios de e analisar os valores de correspondentes e, por fim, traçarmos um gráfico... mas isso seria muito trabalhoso, né?
Então... outra opção seria a gente selecionar os pontos de interseção com os eixos, identificar as assíntotas verticais e horizontais, e determinar o comportamento da curva em torno desses pontos e assíntotas.
Então bora lá!!
😉
Passo 2
Dessa forma, vamos começar encontrando os pontos de interseção com os eixos e :
- Interseção com o eixo (fazendo ):
- Interseção com o eixo (fazendo ):
Como o discriminante é negativo, as raízes são números complexos não reais e não afetam o gráfico no plano .
Portanto, a função não possui interseções com o eixo real.
Agora, vamos calcular as assíntotas verticais e horizontais.
Passo 3
As assíntotas verticais ocorrem quando o denominador se anula, ou seja:
Assim, temos duas possíveis assíntotas verticais em:
E
Passo 4
Por outro lado, quando tende ao infinito, o comportamento do gráfico se aproxima de uma assíntota horizontal.
Dessa forma, as assíntotas horizontais ocorrem quando o grau do numerador é menor ou igual ao grau do denominador.
Logo, para encontrar a assíntota horizontal, basta comparar os graus do numerador e denominador:
Assim, temos uma assíntota horizontal em .
Passo 5
Com essas informações, podemos plotar o gráfico:
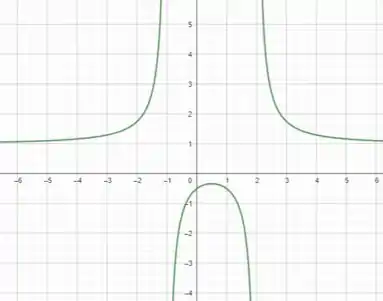
O gráfico terá uma assíntota horizontal em , e duas assíntotas verticais em e .
O ponto de interseção com o eixo é em , mas não há interseção real com o eixo .
Entendeu direitinho? Responde aee ;)
Resposta
