UFCG, Sem Campus, Cálculo Diferencial e Integral I, Listas Cálculo 1 - UAMat - Lista 4 - Aplicação de Derivadas, Questão 4c.
Esboce o gráfico
Passo 1
Oiee bora resolver essa comigo?
Irei descrever como podemos esboçar o gráfico da função
Aqui estão os passos para esboçar o gráfico:
Encontraremos o domínio da função: Para determinar o domínio da função, você precisa encontrar os valores de para os quais o denominador não é igual a zero, pois a divisão por zero não é definida.
Portanto, o domínio é (todos os números reais) exceto
Encontre os pontos onde a fun��ão cruza o eixo
Para temos:
Isso ocorre quando porque qualquer número dividido por ele mesmo é igual a 1, e não pode ser igual a -1 devido ao domínio restrito.
Portanto, o único ponto em que a função cruza o eixo
Passo 2
Encontraremos o comportamento da função para tendendo ao infinito positivo e negativo:
À medida que tende ao infinito positivo, o termo se torna dominante, e a função se aproxima de
À medida que tende ao infinito negativo, o mesmo comportamento ocorre, e a função se aproxima de
Encontre o comportamento da função em relação à assíntota vertical:
Devido ao fator no denominador, a função tem uma assíntota vertical em .
Isso significa que a função se aproxima infinitamente de à medida que se aproxima de -1 pelo lado esquerdo e se aproxima infinitamente de à medida que se aproxima de -1 pelo lado direito.
Passo 3
Agora, você pode esboçar o gráfico com essas informações:
- O domínio da função é exceto
- A função cruza o eixo x no ponto
- A função se aproxima de 1 à medida que tende ao infinito positivo ou negativo.
- A função tem uma assíntota vertical em
O gráfico será uma curva que se aproxima da linha horizontal à medida que se afasta de -1 em ambas as direções e cruza o eixo x no ponto
O gráfico não toca a linha devido à exclusão do ponto do domínio.
Passo 4
Gráfico
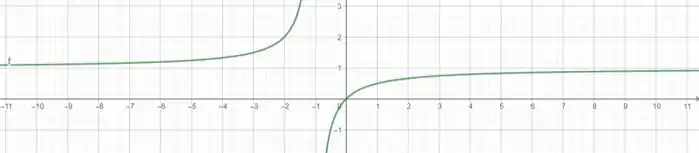
Resposta
Vide o passo a passo.