UFCG, Sem Campus, Cálculo Diferencial e Integral I, Listas Cálculo 1 - UAMat - Lista 4 - Aplicação de Derivadas, Questão 4e.
Esboce o gráfico
Passo 1
E aí meus amores, bora para mais uma?
Para esboçar o gráfico da função
siga os seguintes passos:
Vamos encontrar o domínio da função:
A função é definida para todos os números reais, o que significa que seu domínio é .
Encontraremos os pontos de interseção com o eixo x
Para encontrar onde a função cruza o eixo x, defina
No entanto, a exponencial nunca é igual a zero para qualquer valor real de
Portanto, a função não cruza o eixo x, o que significa que não há pontos de interseção com o eixo x.
Passo 2
Encontre o comportamento da função para tendendo ao infinito positivo e negativo:
À medida que tende ao infinito positivo ou ao infinito negativo o termo no expoente se torna muito grande. Como resultado, se aproxima de zero rapidamente. Isso significa que a função se aproxima de zero tanto para quanto para
Encontre o valor máximo da função:
A função não possui um valor máximo global, pois está sempre decaindo à medida que se afasta do eixo vertical.
No entanto, o valor máximo local ocorre em onde
Passo 3
Agora, você pode esboçar o gráfico com essas informações:
- O domínio da função é , abrangendo todos os números reais.
- A função não cruza o eixo x, pois não há soluções para
- À medida que tende ao infinito positivo ou negativo, a função se aproxima de zero rapidamente.
- O valor máximo local ocorre em , onde
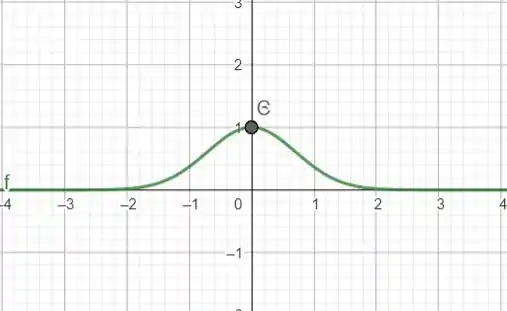
O gráfico será uma curva suave que começa em no ponto e diminui rapidamente à medida que se afasta do eixo vertical em ambos os lados.
Passo 4
Gráfico
Resposta
Vide a explicação.