Esboce o gráfico
Passo 1
Falaiii galerinha do Responde ai
Bora resolver mais uma comigo?
Claro, vou descrever como você pode esboçar o gráfico da função
Aqui estão os passos para esboçar o gráfico:
Encontraremos os pontos críticos da função. Isso ocorre onde a derivada da função é igual a zero.
A derivada de é:
Agora, resolva para encontrar os pontos críticos:
Fatorando:
Isso nos dá duas soluções:
a)
b)
Portanto, existem dois pontos críticos:
Passo 2
Encontraremos os valores de nos pontos críticos e nos pontos onde a função cruza o eixo
Para
Para ;
Passo 3
Encontraremos o comportamento da função para tendendo ao infinito positivo e negativo:
À medida que tende ao infinito positivo ou negativo, o termo domina a função, e os outros termos se tornam menos significativos.
Isso significa que a função se aproxima de à medida que tende ao infinito positivo e se aproxima de à medida que tende ao infinito negativo.
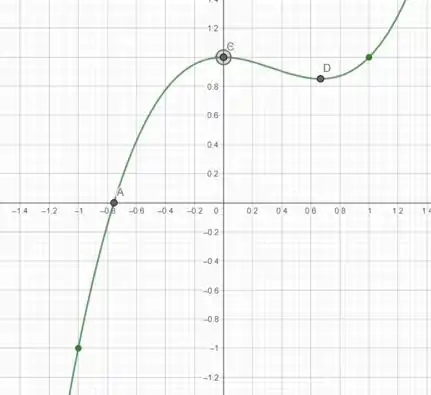
Agora, você pode esboçar o gráfico com essas informações:
- A função passa pelo ponto (0, 1).
- A função possui um ponto crítico em
- À medida que \(x\) tende ao infinito negativo, a função vai para
- À medida que \(x\) tende ao infinito positivo, a função vai para
O gráfico será uma curva suave que passa pelo ponto (0, 1), atinge um mínimo local em e se estende infinitamente para cima e para baixo nos dois lados do eixo x.
Passo 4
Gráfico
Resposta
Vide a explicação.