Esboce o gráfico
Passo 1
Bora resolver mais uma comigo?
Para esboçar o gráfico da função
siga os seguintes passos:
Encontre os pontos de interseção com o eixo
Para encontrar onde a função cruza o eixo x, defina
Fatorando:
Isso resulta em duas soluções:
Para , podemos encontrar as raízes:
Portanto, os pontos de interseção com o eixo x são
Passo 2
Encontre o comportamento da função para tendendo ao infinito positivo e negativo:
À medida que tende ao infinito positivo ou negativo, o termo se torna dominante na função.
Como resultado, a função se comporta como e aumenta infinitamente positivamente quando tende ao infinito positivo e infinitamente negativamente quando tende ao infinito negativo.
Encontre os valores máximos e mínimos locais:
Para encontrar os valores máximos e mínimos locais, podemos calcular a derivada da função e encontrar os pontos onde a derivada é igual a zero.
A derivada de é:
Igualando a zero:
Fatorando em comum:
Isso resulta em duas soluções:
Para , podemos encontrar as raízes:
Portanto, os valores máximos e mínimos locais ocorrem em
Passo 3
Avaliando nesses pontos:
Portanto, temos os seguintes pontos de máximo e mínimo locais: e
Agora, você pode esboçar o gráfico com essas informações:
- Os pontos de interseção com o eixo x são
- À medida que tende ao infinito positivo ou negativo, a função aumenta infinitamente positivamente ou negativamente.
- Os valores mínimos locais ocorrem em , e há um máximo local em
O gráfico será uma curva suave que passa pelos pontos de interseção com o eixo x, atinge um mínimo local em um máximo local em e depois um mínimo local em enquanto se comporta como uma função cúbica no infinito.
Passo 4
Gráfico
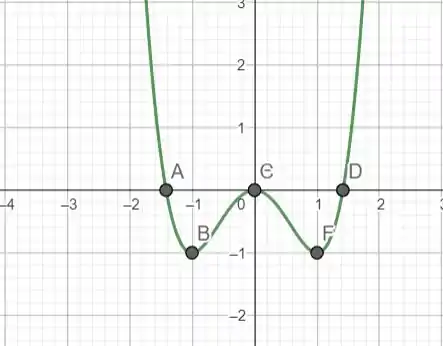
Resposta
Vide o passo a passo.