UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista sobre Derivadas, Questão 8.22
Esboce o gráfico da função
.
Passo 1
Eaew, belezinha?
Temos que esboçar o gráfico da função
Para isso, vamos identificar se a função possui algum ponto de descontinuidade e também verificar quais são os pontos de máximos,mínimos e pontos de sela nos intervalos que ela é contínua. Isso vamos olhar para a derivada da função.
Então vamos lá!
Passo 2
Primeiro vamos verificar se a função é descontínua em algum ponto, ou seja, se temos singularidades. Olhando para a função, temos que ela é descontínua , pois temos um zero no denominador
Então, vamos olhar para o intervalo , no qual a função é contínua.
Passo 3
Temos que quando a derivada é positiva, a função é crescente, e quando a derivada é negativa a função é decrescente. Vamos tomar a derivada da função utilizando a regra do quociente:
.
Para analisar o sinal dessa derivada, vamos notar que o denominador será sempre positivo e também que no intervalo que estamos analisando e . Assim, temos que nesse intervalo a derivada será sempre negativa, sendo então a função decrescente.
Passo 4
Por último, temos que a função é nula para . Assim, como ela é decrescente em todo intervalo de , temos que seu esboço será
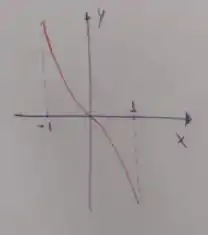
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da questão.