USP– Cálculo 1 – Lista 2 – Questão 1.8eParte2
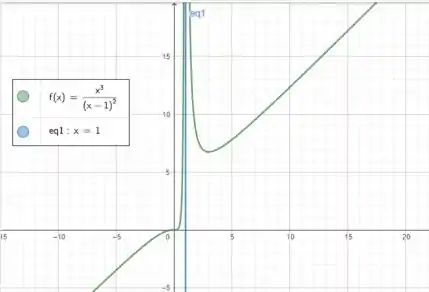
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos dá essa função aqui
Agora nessa parte dois vamos determinar as assíntotas!
- Assíntotas horizontais são quando fazemos o limite da função para e achamos um valor finito . A equação vai ser do tipo
- Assíntotas verticais são quando calculamos o limite da função para um ponto de indeterminação e temos como resultado o infinito. A equação será do tipo
E juntando isso com todos os itens encontrados na parte 1, vamos poder esboçar o gráfico bem bonitinho!
Recordando o que achamos na parte 1:
- Crescente:
- Decrescente:
- Ponto de inflexão: e
- Ponto de mínimo:
- Côncava para cima:
- Côncava para baixo:
- Crescente:
- Decrescente:
- Ponto de inflexão: e
- Ponto de mínimo:
- Côncava para cima:
- Côncava para baixo:
- Não possui assíntotas horizontais
- Assíntota vertical em
Beleza?
Bora lá!
Passo 2
Nossa função é
Calculando o limite quando , podemos desconsiderar aquele do denominador
E para podemos proceder de forma similar
Ou seja, não temos assíntotas horizontais!
Beleza?
Passo 3
Agora vamos analisar os possíveis pontos de descontinuidade da função
Como temos um denominador que zera em precisamos analisar os limites em torno desse ponto!
Temos uma assíntota vertical em
Passo 4
Bora construir o gráfico?
Ela tem de características:
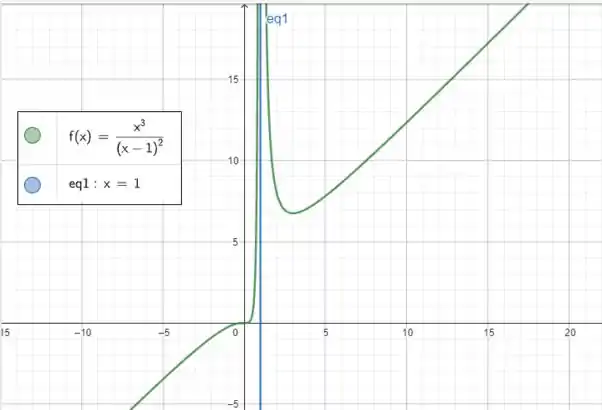
E é isso! Até mais!
Resposta
