USP– Cálculo 1 – Lista 2 – Questão 1.8k
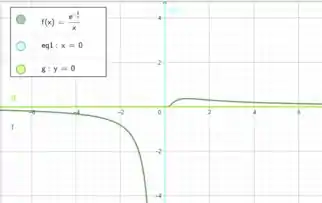
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos dá essa função aqui
Agora nessa parte dois vamos determinar as assíntotas!
- Assíntotas horizontais são quando fazemos o limite da função para e achamos um valor finito . A equação vai ser do tipo
- Assíntotas verticais são quando calculamos o limite da função para um ponto de indeterminação e temos como resultado o infinito. A equação será do tipo
E juntando isso com todos os itens encontrados na parte 1, vamos poder esboçar o gráfico bem bonitinho!
Recordando o que achamos na parte 1:
- Crescente:
- Decrescente:
- Ponto de máximo:
- Côncava para baixo:
- Côncava para cima:
- Crescente:
- Decrescente:
- Ponto de máximo:
- Côncava para baixo:
- Côncava para cima:
- Assíntota vertical: pela esquerda
- Assíntota horizontal: para os dois lados
Beleza?
Bora lá!
Passo 2
Nossa função é
Calculando o limite quando
Sendo assim para grandes valores de temos uma assíntota horizontal em
Beleza? Agora para
Também temos assíntota horizontal para !
Passo 3
Agora vamos analisar os possíveis pontos de descontinuidade da função
Como temos que o denominador zera em , precisamos analisar o limite da nossa função para e para
Temos que . Agora para :
Sendo assim temos uma assíntota vertical pela esquerda em
Passo 4
Bora construir o gráfico?
Ela tem de características:
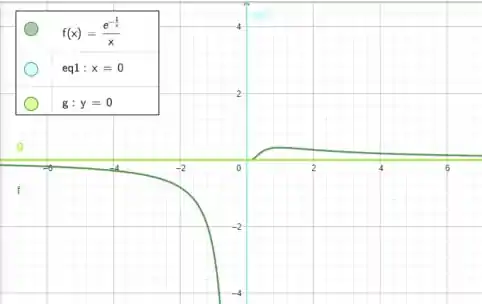
E é isso! Até mais!
Resposta
