Esboce o gráfico de .
Para que valores de a curva corta a reta ?
Passo 1
Nós temos que dividir a análise do gráfico em domínio, análise do crescimento, análise de concavidade e assíntotas. Começamos no domínio:
Como a gente vê, não há fator limitante para o domínio. Nosso domínio vai ser:
Há ainda uma relação de paridade, já que para qualquer valor de . Isso significa que a função será espelhada em relação ao eixo .
Passo 2
Vamos observar o crescimento da função; para isso analisamos o sinal da derivada primeira. Vamos derivar o termo pela Regra do Produto e da cadeia:
Como a exponencial é sempre positiva e a parábola não possui raízes reais (pode aplicar Bhaskara para ver isso) e tem concavidade para cima nós vemos que o sinal da derivada vai depender só do , que é positivo para e negativo para !
A função é decrescente em e crescente em . será o único ponto crítico, que consistirá em um máximo local, já que a derivada é positiva antes e negativa depois.
Passo 3
Vamos olhar a derivada segunda agora e a concavidade. Vamos, novamente pela Regra do Produto:
Para esse termo, se chamarmos , teríamos a parábola . Por Bhaskara, acharíamos as raízes e . Como queremos só soluções reais, os valores de que zeram esse termo serão:
Serão pontos de inflexão. Fazemos a seguinte divisão polinomial:
Então o termo da derivada segunda pode ser escrito como:
Podemos fazer o quadro de sinais para esse cara, já lembrando que a exponencial e o são positivos e o sinal só depende do e do .
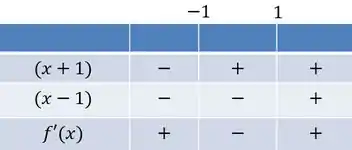
A gente vai reparar que a concavidade é para cima quando e para baixo quando está em .
Ponto de inflexão em , .
Passo 4
Assíntotas agora. As verticais estão relacionadas com as descontinuidades, ou seja, não teremos nenhuma delas para essa função.
Para assíntotas horizontais temos que lançar o limite para e :
Uma assíntota horizontal em , para os . Assim, não haverão assíntotas oblíquas.
Passo 5
Agora reunimos as informações que já achamos:
Vamos para o esboço, sendo e :
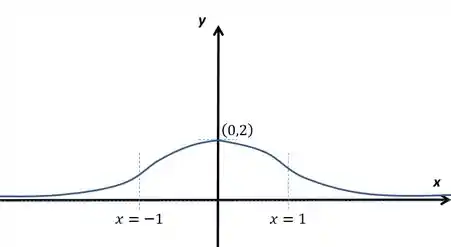
Passo 6
Vamos igualar as equações para :
Repara é como se fosse o que vimos na letra . A imagem da função, segundo o gráfico, vai de , sem nunca assumir esse valor, até , valor máximo no ponto . Ou seja, os valores de que gerariam um encontro entre as curvas sãos os valores de que correspondam ao seguinte: