Nos exercícios a esboce o gráfico da função.
Passo 1
Eaew, tudo certinho contigo?
Temos a seguinte função
queremos esboçar o seu gráfico! Então iremos ter que analisar diversas características! Como, intervalos de crescimento, decrescimento, máximos, mínimos, domínio, quando a função se anula, assim por diante! Vamos ao longo dos passos avaliar tudo que é possível! Vem comigo!
Passo 2
Primeiro, temos alguma limitação sobre o domínio da função? Não, não temos, é uma função exponencial e esta é uma função que nunca é negativa, mas que tem um valor determinado para todo . Mas, e então? Que diferença entre a exponencial
e a exponencial
A principal mudança está na presença de uma assíntota horizontal em . Note que
ou, resumindo
que é uma assíntota horizontal em . mas, quando tentamos fazer o mesmo para a expressão com o módulo no expoente, temos que
ou seja
que não é mais uma assíntota horizontal! Note então que termos o gráfico da exponencial espelhado em que é quando o expoente se tornaria negativo, da seguinte maneira
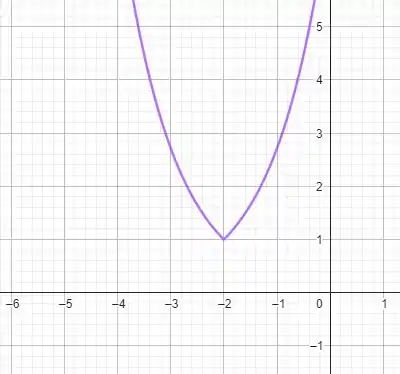
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!