UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 10.1b
Faça um estudo qualitativo das funções dadas a seguir. Em seguida, esboce seus gráfico, desta-
cando os pontos de máximo e mı́nimo locais e/ou globais, pontos de inflexão e assíntotas (caso
existam).
Passo 1
Eaew, belezinha?
Para fazer um estudo qualitativo da função, vamos estudar sua derivada, que nos dá os intervalos em que a função cresce, decresce e seus pontos de extremo. Também vamos verificar o comportamento da função quando a variável x vai à ou e procurar pontos onde f(x) vai a infinito. De cara, olhando para o denominador da função, vemos que, no intervalo [-1,1] a função não possui valor real, pois temos um denominador que será ou nulo ou então a raíz de um número negativo. Então, vamos restringir o estudo da função no intervalo . Vamos lá então?
Passo 2
Primeiramente, vamos calcular a derivada da função f(x). Identificando as funções e , podemos escrever a derivada de f(x) através da regra do quociente. Como e , podemos escrever a derivada de f(x) como
Como fora do intervalo [-1,1] o denominador é sempre positivo, quem irá ditar o sinal da derivada e, consequentemente, se a função cresce ou decresce, é o numerador. Então, a gente quer determinar em quais intervalos a derivada é positiva, em quais ela é negativa e se ela é nula em algum ponto. Primeiro vamos procurar o intervalo onde a derivada seja nula ou positiva. Para isso, fazemos
Multiplicando os dois lados da desigualdade por , obtemos
Com isso, chegamos ao resultado absurdo de que -1 é maior ou igual à zero! Então, não existe nenhum valor de x para o qual a função seja crescente ou tenha um ponto de extremo. Em todos os pontos, sua derivada é negativa. Agora, vamos analisar o que acontece com a função quando ela se aproxima dos limites do intervalo . Bora lá!
Passo 3
Para estudar o limite da função quando ela vai a infinito, primeiro colocaremos o termo do denominador em evidência.
Assim, se tiramos o limite da expressão acima, vamos ter que o termo irá à zero tanto quando x for a mais infinito quanto para menos infinito. Então, no limite , temos que, em módulo
Devido ao sinal do numerador, para valores negativos de x, temos que a função tende à -2 enquanto que para valores positivos de x, a função tende a 2. Logo, temos duas assíntotas horizontais: , pois a função tende mas nunca atinge esses valores. Agora, para os valores da função quando x se aproxima de , temos que o denominador será muito próximo de zero, de modo que a função, em módulo, terá um valor muito grande. Mas, há uma pequena diferença devido ao numerador: o numerador 2x irá ditar o sinal da função e, portanto, se ela tende à mais ou a menos infinito. No caso de , temos
E para Recapitulando tudo que concluímos até aqui: temos uma função que, quando está próxima de -2 e sempre decrescendo conforme aumentamos x. Quando x se aproxima de -1, a função tende a rapidamente. Aí, no intervalo [-1,1], a função não está definida. Quando x está bem próximo de 1 pelo lado esquerdo, a função tende à , mas sempre decrescendo. Até que, quando , a função tende à 2 mas nunca alcança esse valor. Então, temos que essa função possui duas assíntotas horizontais () e duas assíntotas verticais, onde seu valor vai em módulo à infinito. Dá uma olhada em como é gráfico da função:
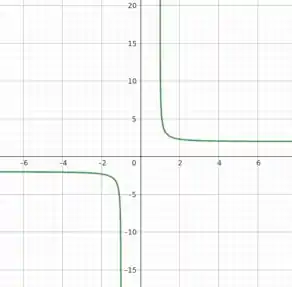
Resposta
No decorrer da questão.