Faça um estudo qualitativo das funções dadas a seguir. Em seguida, esboce seus gráfico, desta-
cando os pontos de máximo e mı́nimo locais e/ou globais, pontos de inflexão e assíntotas (caso
existam).
Passo 1
Eaew, belezinha?
Para fazer um estudo qualitativo da função, vamos estudar sua derivada, que nos dá os intervalos em que a função cresce, decresce e seus pontos de extremo. Também vamos verificar o comportamento da função quando a variável x vai à ou e procurar pontos onde f(x) vai a infinito. De cara, olhando para o denominador da função, vemos que, a função não possui valor definido para os pontos x = -2 e x = 3, pois nesses pontos temos um denominador que será nulo. Então, vamos dá uma olhada no comportamento da função nos intervalos de . Bora lá?
Passo 2
Primeiramente, vamos calcular a derivada da função f(x). Identificando as funções e , podemos escrever a derivada de f(x) através da regra do quociente. Como e , podemos escrever a derivada de f(x) como
Como no denominador temos dois termos quadráticos que nunca são negativos, quem irá ditar o sinal da derivada e, consequentemente, se a função cresce ou decresce, é o numerador. Então, a gente quer determinar em quais intervalos a derivada é positiva, em quais ela é negativa e se ela é nula em algum ponto. Primeiro vamos procurar o intervalo onde a derivada seja nula ou positiva. Para isso, fazemos
Portanto, para que a derivada seja positiva ou nula temos que o último termo em parênteses deve ser negativo ou nulo: . Isso é impossível para valores reais de x, pois é sempre positivo, e assim, sua adição com 1 nunca pode ser negativa ou nula. Então, a gente tem uma função que em todos os pontos sempre possui derivada negativa! Ela sempre decresce. Agora, com isso em mente, só precisamos determinar suas assíntotas horizontais e verticais para ter um esboço da função. Quer saber como fazer isso? Então, vamo lá!
Passo 3
Agora, vamos estudar o limite da função quando ela vai a infinito, primeiro vamos escrever a função de uma outra forma:
Como no numerador temos um polinômio de primeiro grau e no denominador temos um polinômio de segundo grau (que cresce mais rapidamente que o de primeiro), temos que, quando x for a infinito, o denominador será muito maior que o numerador, de modo que a função será quase nula, mas nunca exatamente nula. Igualmente, quando x for à menos infinito, a mesma coisa ocorre. Em outras palavras:
Bem, já temos o comportamento da nossa função no infinito. Agora vamos analisar o comportamento dela por partes do nosso intervalo : se viermos de até -2, o que acontece com a função? Bem, a gente sabe que em ela está muito próxima de zero e que, como a derivada é sempre negativa, a função sempre decresce. Até que ela se aproxima de -2. E aí o que acontece com a função quando nos aproximamos de -2? Vamos calcular o limite!
Como discutido anteriormente, a gente sabe que o denominador vai a zero e, assim, a função explode! Maas, quando nos aproximamos pela esquerda de -2, a função está sempre abaixo de zero e, portanto negativa. Assim, a função vai à . Agora, quando nos aproximamos de -2 pela direita, a função também explode mas positivamente! Mas por quê? Porque o termo (x+2) vai ser muito próximo de zero mas vai ser positivo, já que pela direita de -2 os valores de x são menores em módulo que -2 e, assim (x+2) é maior que zero. Quando x chega a zero a função é nula e, como a derivada é sempre negativa, conforme vamos aumentando x, ela continua decrescendo até que nos aproximamos pela esquerda de outro ponto de interesse: x=3. Nesse ponto, novamente a função não está definida, porque o denominador vai a zero, o que leva a função à explodir. Mas como estamos nos aproximando de x=3 por valores menores que 3, temos que (x-3) é negativo, de modo que, a função vai a menos infinito ao invés de ir a infinito. Agora, para terminar, só precisamos determinar o que acontece no intervalo (3,). Quando nos aproximamos de x=3, dessa vez pela direita e, então, com valores um pouco maiores que 3, temos que (x-3) no denominador será próximo de zero, mas positivo, pois os valores de x são maiores que 3. Assim, pela direita de x =3, a função vai à . A partir daí, ela vai decrescendo, já que sua derivada é sempre negativa até que, ela tende a zero quando . Assim, temos que a nossa função tem uma assíntota horizontal: a reta y = 0, a qual ela nunca alcança para . A função também possui duas assíntotas verticais: x = -2 e x = 3. Quando a função se aproxima desses valores ela explode, de modo que não está definida para nenhum deles. Dá só uma olhada no gráfico da função!
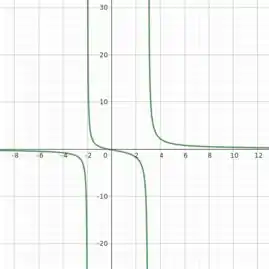
Resposta
No decorrer da questão.