UFRJ – Cálculo 1 – Lista 3 – Questão 9
A figura mostra os gráficos de . Identifique cada curva e explique suas escolhas.
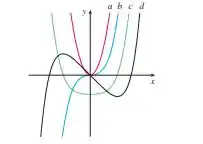
Passo 1
Fala aí, galera!!! Tranquilidade aí com vocês?
Vamos olhar inicialmente pra curva d. Se você perceber, quando temos um ponto na curva d com reta tangente HORIZONTAL, a curva c terá valor de 0. Isso mostra pra gente que a curva d é a função . Por sua vez quando c possui um ponto com reta tangente horizontal, b vale 0. O que implicará em dizer que e . E quando b possui um ponto com reta tangente horizontal “a” vai valer 0, ou seja
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2