6. Uma folha de papelão mede . Dois quadrados iguais, de lado , são recortados dos vértices de um lado com , como mostra a figura. Dois retângulos iguais são recortados dos outros vértices, de modo que as abas possam ser dobradas para formar uma caixa retangular com tampa.
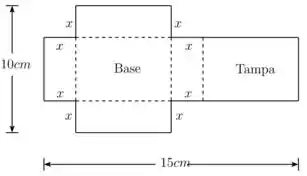
(a) Escreva uma fórmula para o volume da caixa.
(b) Determine o domínio de .
(c) Determine o valor de para que o volume da caixa seja o maior possível.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão estamos interessados em obter a fórmula do volume para uma caixa de altura e que as medidas da folha de papelão deve ser por cm.
Alguma ideia do que fazer? 🤔
O volume de uma caixa é dada pela área da base multiplicada pela altura.
Porém, as dimensões da folha de papelão que usamos é limitada a por , então não podemos usar qualquer valor.
Vamos ver como fica na prática? 😁
Passo 2
A área da base do papelão é dada por
Usamos no lugar de pois para a caixa fechar, é necessário que a haja uma tampa de mesmo tamanho da base.
Já o volume é dado pela área da base multiplicada pela altura, ou seja
Para obter o domínio de vamos olhar para a equação da área da base
nunca pode ser negativo, portanto, deve ser maior ou igual a e menor ou igual a . Pois se for maior que , o termo fica negativo e fisicamente é como se estivéssemos tirando parte da área da tampa para usar na base, o que não pode acontecer.
Tranquilo até aqui? 👀
Passo 3
Para obter o valor de para atingir seu maior valor, temos que obter os pontos críticos de e ver qual é o ponto cuja imagem de é maior.
Obtendo as raízes dessa função, chegamos em
Ou aproximadamente e .
No item anterior, vimos que tem que estar entre e , portanto está descartado e o ponto que nos dá o maior volume é quando
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta
a)
b)
c)