UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 2.10a
A função , aparece em aplicações para a sintetização de frequência modulada (FM).
(a) Use uma calculadora gráfica para esboçar um gráfico da função f (x), em seguida, use esse gráfico para dar um esboço, mesmo que grosseiro, do gráfico de sua derivada f ′ (x).
Passo 1
Eaew, belezinha?
Temos que traçar o gráfico de uma função:
E então fazer um esboço grosseiro de sua derivada. Vamos lembrar que a derivada é nula nos pontos de máximo, mínimo e de sela. Além disso, temos que a derivada é positiva quando a função é crescente, e é negativa quando a função é decrescente. Então vamos lá!
Passo 2
Temos que a função:
Fizemos o esboço utilizando uma calculadora gráfica:
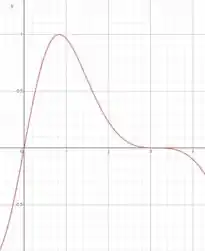
Passo 3
Agora utilizando as informações que mencionamos no passo 1, vamos fazer um esboço do gráfico da derivada dessa função:
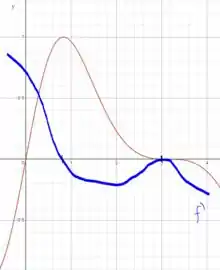
Note que temos um ponto máximo e um ponto de sela, nestes a derivada é nula. A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da questão.