Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Esboço de Gráfico

Ver Teoria
Exercício 239123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 2.10b

A função f   ( x ) = s e n   ( x + s e n   ( x   ) ) ,   0 < x < π , aparece em aplicações para a sintetização de frequência modulada (FM).

(b) Calcule f′(x) e utilizando uma calculadora gráfica plote seu gráfico. Compare com o obtido no item (a).

Passo 1

Eaew, belezinha?

Temos que derivar a função:

f   ( x ) = s e n   ( x + s e n   ( x   ) ) ,   0 < x < π

E então fazer um esboço do gráfico de sua derivada. Então vamos lá!

Passo 2

Temos que a função:

f   ( x ) = s e n   ( x + s e n   ( x   ) )

Utilizando a regra da cadeia, tomamos sua derivada:

f ' ( x ) = c o s   ( x + s e n   ( x   ) ) ( 1 + c o s ( x ) )

Passo 3

Agora utilizando uma calculadora gráfica, vamos fazer um esboço do gráfico da derivada dessa função:

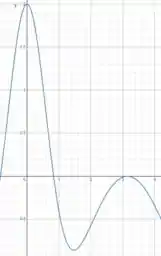
Comparando com o do item anterior, temos que ambos possuem comportamentos semelhantes.

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

No decorrer da questão.

Exercícios de Livros Relacionados

Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2