O gráfico da derivada é dado a seguir:
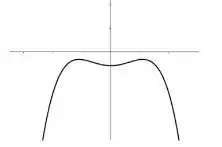
Qual das seguintes alternativas corresponde ao gráfico de ?
Passo 1
Opa galera, aqui é uma questão de cálculo diferencial onde nós temos uma função qualquer que está definida e bem comportada ao longo de um certo domínio uma vez que pelo gráfico podemos enxergar que a função é diferenciavel em todos os pontos, logo ela também é continua nesses pontos.
Para resolver o probleminha precisamos lembrar de um certo detalhezinho sobre as derivadas de primeira ordem de uma função. Mas eis a pergunta, você se lembra?

CAAAAAAAAAALMINHA, não precisa se preocupar vamos lembrar desse conceito bem importante aqui, o conceito físico sobre as derivadas de primeira ordem fala o seguinte:
Ok,ok né? Como isso me ajuda a resolver a questão? Simples, vamos olhar o gráfico da derivada disponibilizada pela questão e vamos desenhar um esboço para melhor visualizar.

Já deve estar na sua mente, não bastava cálculo, mas agora tenho que desenhar? AFFF
Mas rlx esse desenho aqui é simpleszinho e eu irei desenhar com você passo a passo.
Passo 2
Aqui vamos analisar a seguinte imagem:
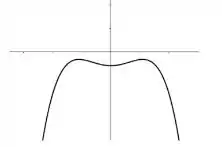
Se você perceber bem a curva dessa derivada ela começa de uma forma crescente então a derivada deve crescer conforme o x aumenta de valor. Então a região deve ser crescente nessa região até chegar em uma região que parece uma montanha pequena que aparenta que a derivada se anula.
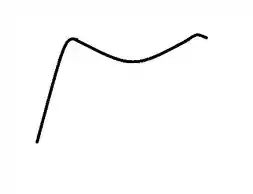
O início da função deve ser algo assim:

Depois o valor da derivada começa a diminuir, o que indica que nessa região a função deve ser decrescente e depois volta a crescer novamente até chegar em outro patamar que a derivada zera. Logo o nosso gráfico deve ficar assim:
E para finalizar a derivada retorna a diminuir novamente então finalizando a nossa curva:
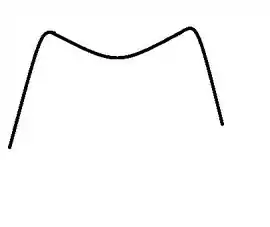
Resposta
Analisando o gráfico que nos compomos a alternativa que melhor se ajusta ao desenho é a letra