3) repita o que foi feita no feito no exercício acima para as funções seguintes;
e)
Passo 1
Fala aí, galerinha!! Nesse exercício ele pede para a gente obter uma série de coisas:
- Pontos críticos,
- Máximos e mínimos locais,
- Intervalos de crescimento e decrescimento,
- Pontos de inflexão,
- Intervalos onde é côncava para cima e para baixo
- Determinar as (possíveis) assíntotas
- Fazer um esboço do gráfico.
NOSSA! Um monte de coisa... mas relaxa que a gente fazendo cada um dos passos aqui isso vai sair bem de boa. Todos esses itens estão relacionados com as derivadas da função. Então a gente começa calculando essas derivadas! No geral a primeira derivada dá conta da maioria dos itens, mas não vamos esquecer que a segunda derivada também ajuda bastante então é legal começarmos calculando as duas!
Passo 2
Vamos começar calculando as derivadas de
Nós temos uma função composta então a gente usa a regra da cadeia:
Passo 3
Também é bem útil começar obtendo a derivada de segunda ordem. Fazemos isso derivando a função:
Agora temos uma divisão de funções. A gente resolve essa derivada usando a regra do quociente:
Então temos
Showw, agora a gente usa essas derivadas nos testes para obter cada um dos itens que nos pediram!
Passo 4
Vamos começar com os pontos críticos. Esses pontos são aqueles em que a primeira derivada é zero:
Aqui temos uma única possibilidade
Então temos um único ponto crítico em
Passo 5
Uma vez que a gente possui as derivadas e o nosso ponto crítico vamos classificar esse ponto em um máximo ou mínimo local ou em um ponto de inflexão. Para ver se é um máximo ou mínimo local, vamos ver o sinal da segunda derivada nesse ponto:
Como a segunda derivada no ponto crítico é positiva, é um mínimo local de !
Como essa função não possui outros pontos críticos, não temos um máximo local e nem um ponto de inflexão!
Passo 6
Para ver sobre o intervalo de crescimento ou decrescimento olhamos os sinais de . Quando esse cara é positivo, a função é crescente e quando é negativo a função é decrescente.
Vamos olhar a cara de
Como o denominador é sempre positivo, quem dita o sinal dessa função é o termo então temos
- quando e a função é crescente nesse intervalo;
- quando e a função é decrescente nesse intervalo.
Passo 7
Agora, para olhar sobre a concavidade, olhamos o sinal da segunda derivada
Aonde temos a regra:
A gente pode perceber que a função tem um número positivo e um denominador que é um quadrado de um polinômio . Esse último termo é sempre positivo então quem dita o sinal de é
A função vai ser concava para cima quando:
Ou seja, no intervalo
E vai ser concava para baixo quando
Ou seja, quando:
Como a função muda a concavidade em e esses são os pontos de inflexão da função!
Passo 8
Para olhar as assíntotas a gente deve olhar dois casos:
Assíntotas verticais: Quando temos um onde
Quando a nossa função é um log , ela diverge quando seu argumento é nulo. Então a a assíntota é dado pela equação:
E aí a gente percebe que não vamos ter nenhum que resolva essa equação. Então não temos assíntotas verticais para essa função!
Assíntotas horizontais: A gente calcula os limites:
Quando isso acontece, não temos nenhuma assíntota horizontal.
Passo 9
Para esboçar essa função a gente junta todas essas informações que a gente obteve. Primeiro marcamos o mínimo local em , marcamos os pontos de inflexão e esboçamos através da concavidade dessa função lembrando os intervalos de crescimento da função. A gente fica com algo assim:
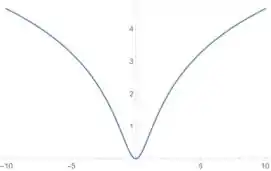
Resposta