Repita o que foi feito no exercício acima para as funções seguintes.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou te ajudar!
O problema nos deu essa função aqui
E pediu para determinarmos várias coisas! Aqui vou fazer um resumo de cada uma dessas coisas e como encontramos cada uma delas:
- Pontos críticos: pontos onde a derivada é nula
- Máximos e mínimos locais: pontos onde a derivada apresenta troca de comportamento (de positivo/negativo para negativo/positivo)
- Intervalos de crescimentos e decrescimento: crescimento – intervalo onde a derivada é positiva, decrescimento – intervalo onde a derivada é negativa
- Pontos de inflexão: onde a segunda derivada é zero
- Concavidade da função: côncava para cima – derivada segunda positiva; côncava para baixo – derivada segunda negativa;
- Assíntotas verticais: pontos em que o denominador da função é zero; Assíntotas horizontais: comportamento da função quando
Anota aí!

E é tudo isso que vamos fazer! Vamos começar analisando as assíntotas, depois analisando a derivada primeira, a derivada segunda e por fim construir esse gráfico bem bonitão!
Mas relaxa que vou fazer passo a passo com você!
Vamos começar?
Passo 2
Nossa função é
Existir assíntota vertical depende de termos uma descontinuidade da função. Vemos que nosso denominador tem um , e quando temos uma indeterminação! Isso significa que temos uma assíntota vertical em
Precisamos analisar a função em torno desse ponto (limite sanduíche), assim conseguimos fazer um esboço com mais clareza! Aqui é só olhar o sinal da função, aí já conseguimos descobrir se vai para ou :
 beleza?
beleza?
Para verificar assíntotas horizontais precisamos calcular o limite da função quando , beleza? Vamos começar com
Olhando para o temos que a função tende a , então aqui não temos uma assíntota horizontal. Fazendo de forma análoga, vamos encontrar também quando , então não temos assíntotas horizontais para os dois lados!
Beleza?
Embora não tenhamos assíntotas horizontais, essa análise do sinal é importante e você vai ver mais pra frente!
bora analisar a derivada primeira?

Passo 3
Agora vamos analisar a derivada :
Os pontos críticos são onde a derivada é zero:
Achamos dois pontos críticos!
Agora para classificar se é ponto de máximo ou mínimo, precisamos analisar o sinal da derivada em torno desses pontos. Se houver troca de sinal, podemos ter duas possibilidades
- De negativo para positivo: então esse ponto é de mínimo local
- Se positivo para negativo: esse é um ponto de máximo local
A ideia é testar na derivada um valor antes e um valor depois de cada ponto para saber o sinal que assume

Analisando e
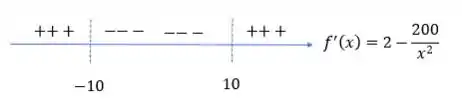
Assim podemos classificar os pontos críticos:

Agora vamos ver o último quesito que envolve a derivada: intervalo de crescimento e decrescimento!
Temos que a função é crescente quando a derivada é positiva, então nesse caso
Beleza?

E decrescente onde ela é negativa:
Atenção: embora a seja negativa entre e , precisamos quebrar esse intervalo! Lembra que em a função não está definida!
Tudo bem até aqui?

Bora para a análise da derivada segunda!
Passo 4
Agora vamos analisar os aspectos que envolvem a derivada segunda! Com a derivada segunda podemos encontrar os pontos de inflexão, ou seja, os pontos onde a concavidade da função muda!
A ideia é análoga ao da derivada primeira: pegar a derivada segunda, igualar a zero e encontrar os pontos que satisfazem isso. Por fim, analisar o sinal da em torno desses pontos e encontrar a concavidade da função
- Derivada segunda positiva: função côncava para cima
- Derivada segunda negativa: função côncava para baixo
Beleza?

Vamos resgatar a derivada primeira do passo anterior:
E derivar novamente
Igualando a zero temos:
Ué, e agora? Será que existe algum valor de que vá zerar isso daí? Não, não existe!
Isso significa que não temos pontos de inflexão!

A única análise que podemos fazer sobre a concavidade é testar em volta da assíntota vertical que achamos no passo 2!
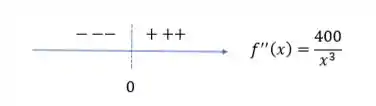
Em resumo temos
Embora tenhamos troca de concavidade, não temos pontos de inflexão! Isso acontece quando temos uma assíntota vertical!
Beleza? Estamos quase lá! Agora é #partiu gráfico!

Passo 5
Nosso passo final é reunir todas as informações e esboçar o gráfico da função!
E nosso gráfico ficou assim:
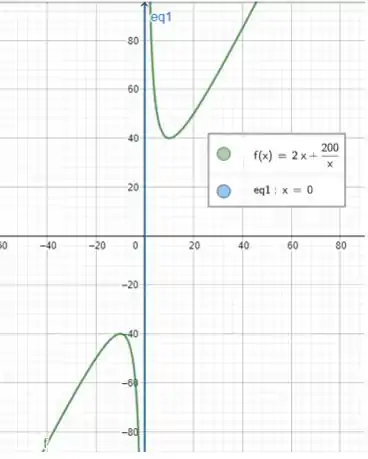
Ufa terminamos!
E é isso! Espero ter ajudado!