Seja
- Determine o domínio da função
- Calcule a derivada da função
- Determine todas as assíntotas da curva . Calcule todos os limites necessários e justifique suas respostas.
- Esboce o gráfico de
Passo 1
Letra a) pra gente analisar o domínio da função, a gente sempre tem que olhar para o ponto que dar ruim. Olha pra função:
Qual ponto que ela dá ruim?
O ! Tem algum outro?
Hummmm! Vejamos, o arco-tangente funciona pra todos os pontos, então é só esse mesmo.
Logo, o domínio da região é toda a reta real tirando o : .
Passo 2
Letra b) bem, nesse item, apenas devemos ficar atentos que se trada de uma derivada de uma fração, ou seja... regra da derivada de frações resolve a nossa vida ;)
Vamos lá, pela regra da fração, temos
Calculando as derivadas desses carinhas no nominador separadamente:
Aplicando a regra da cadeia aqui
A derivada de é , portanto
Como , a gente ganha que a derivada da função toda é
Passo 3
Letra c) Então, vamos começar aqui a procurar as assíntotas horizontais, se lembra como podemos fazer isso?
Não tem problema se não! A gente deve aplicar o limite da função nos infinitos (tanto no positivo, quanto no negativo) se a função tender a um número, bem... essa será a assíntota.
Começando pelo lado positivo, ou seja
Pow, como a gente já sabe, o arco-tangente é uma função limitada porque ela está entre e .
Cara, se isso é verdade, então se o denominador vai para o infinito, então a gente pode falar que o limite vai para.....
A mesma história para o lado negativo da coisa
Então a gente conclui que a reta é uma assíntota horizontal ;)
Passo 4
Pra verificar se há assíntotas obliquas, a gente deveria fazer aquele limite se lembra?
Mas cara, uma grande dica aqui, se a gente calculou os dois limites para assíntotas horizontais, e eles deram um valor, então esse limite aí com certeza vai ser zero, ou seja, pode falar direto que não tem assíntotas oblíquas como é o nosso caso, beleza?
Passo 5
Infelizmente a gente não tem um macete desse para as verticais não, então a gente tem que calcular na marra! Bora?
Pra verificar se tem esse tipo de assíntota a gente deve calcular outros limites, mas dessa vez com o indo para o ponto problemático, veja só
Como o ponto que a função não funciona é o nesse caso, então a gente calcula
Se esses limites forem para o infinito, então será uma assíntota vertical, percebeu?
Passo 6
Então vamos procurar esses limites aí:
Quando vai a , o arco-tangente também vai. Então temos um caso de e podemos aplicar L’hopital, se lembra dele?]
A gente calcula a derivada em cima e em baixo
A derivada de é e a derivada do cima a gente já calculou
Substituindo o ...
Passo 7
Quanto ao outro limite
Vamos aplicar L’hopital novamente...
Ou seja, ele tende para o mesmo número
Como não é nada parecido com um infinito, garantimos que não tem assíntotas verticais !
Passo 8
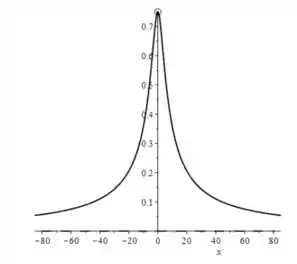
Letra d) Então, pra desenhar o gráfico bastamos colocar todas as informações anteriores no gráfico!
Tipo, sabemos que não tá no domínio, mas quando a função tende a ele, ela cresce para um número .
E que no infinito essa função tende a ! Então essa função, só pode ter essa cara aqui
Resposta
Letra a)
Letra b)
Letra c)
Letra d)