Seja
Com e . Determine, caso existam:
definida para .
- Assíntotas horizontais e verticais do gráfico de
- intervalos onde é crescente e intervalos onde é decrescente
- pontos críticos de
- máximos locais e mínimos locais
- intervalos onde o gráfico de é côncavo para cima e intervalos onde o gráfico de é côncavo para baixo
- pontos de inflexão do gráfico de
- utilizando os resultados dos itens anteriores, esboce o gráfico de
Passo 1
Pra calcular as assíntotas horizontais temos que fazer os limites com . Vamos lá:
Não há assíntotas horizontais.
Passo 2
As assíntotas verticais só existem se a função tiver descontinuidade. Nesse caso, a função é contínua para todo . Por isso, não há assínttoas verticais.
Passo 3
Para saber os intervalos de crescimento e decrescimento temos que analisar o sinal da derivada de .
Tendo esses dois pontos importantes de , podemos fazer o quadro de sinais:
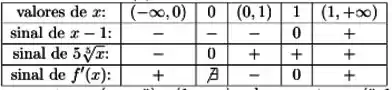
Assim, conclui-se que
Passo 4
Os pontos críticos de ocorrem quando
Vimos no passo anterior que isso ocorre em
Portanto, o único ponto crítico existente é o ponto .
Passo 5
Os pontos candidatos a serem máximos e mínimos são (ponto crítico) e (onde a função não é contínua). Observe o quadro de sinais. Como a derivada muda de positiva para negativa ao se aproximar de , esse é um ponto de máximo local.
No ponto a derivada muda de negativa para positiva, logo este é uma ponto de mínimo local.
Passo 6
Temos que descobrir onde a função é côncava pra cima ou côncava pra baixo. Como fazer isso? Analisando o sinal da segunda derivada
Os pontos significativos para essa função são:
E quando ela não está definida:
Agora podemos fazer o quadro de sinais, que fica assim:

Quando
Quando
Passo 7
Os pontos de inflexão são os pontos onde a função muda de concavidade. Nesse caso, só há um ponto de inflexão, que acontece em
Seu valor é
Passo 8
Juntando tudo que descobrimos nos passos anteriores, e sabendo as interseções com o eixo :
E como eixo :
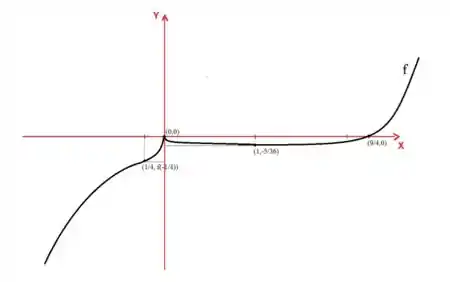
Podemos esboçar o gráfico:
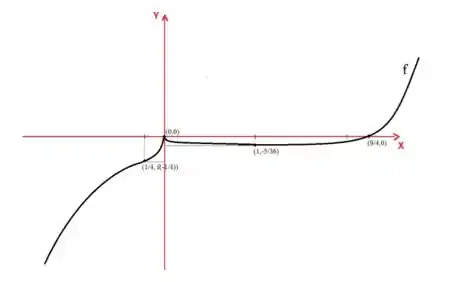
Resposta