Seja
Determine o domínio de
Determine os intervalos de crescimento e os intervalos de decrescimento de
Determine os pontos de máximo e de mínimo de
Determine todas as assíntotas da curva
Determine todos os pontos de inflexão de
Esboce o gráfico de contemplando tudo que foi calculado acima
Considere agora a função A respeito do domínio de , o que se pode afirmar? Escolha uma das opções abaixo e justifique adequadamente a sua resposta.
O domínio é
O domínio é
O domínio é
O domínio é onde
Passo 1
No termo da função não temos nenhum limitante do domínio. Com isso,
Passo 2
Vamos derivar pela Regra do Produto:
Repare que é sempre positivo. Com isso, quem comanda o sinal da derivada e o crescimento da função é o . Fazendo o quadro de sinais com ele:
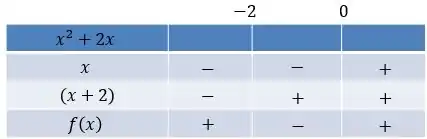
Dado isso, a função será crescente em e decrescente em , como indicado no quadro de sinais da derivada de .
Passo 3
Para analisar os pontos de mínimo e máximo procuramos pontos de mudança do sinal da derivada. Quando vai de positiva para negativa, temos máximo. Quando negativa para positiva, temos mínimo.
Assim, é ponto de máximo e de mínimo.
Passo 4
Procuramos por assíntotas. Sabemos que as verticais estão relacionadas com descontinuidades no domínio. Como o domínio dessa função é composto por todos os números reais, teremos que não existem assíntotas verticais.
Vamos olhar agora por assíntotas horizontais, com :
Sem assíntotas para .
Aplicando L’Hospital
L’Hospital de novo:
Assíntota horizontal em .
Passo 5
Vamos fazer a análise da derivada segunda, que nos dá informações sobre a concavidade do gráfico e seus pontos de inflexão. Achamos a derivada segunda pelas Regras de derivação do Produto e do Quociente:
Zerando essa função, sabendo que sempre:
Logo, os pontos de inflexão são .
Passo 6
Agora, juntando tudo que vimos na questão, temos o seguinte:
Assim, o gráfico será:
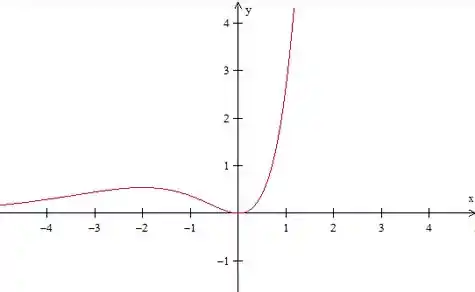
Passo 7
Observando o domínio teremos de , sabemos que a imagem da função será , uma vez que o cosseno é confinado nesses valores por definição.
Assim, o domínio de sua inversa deve corresponder com sua imagem, teríamos o domínio de valendo .
Porém, temos ali o arco cosseno de . Assim, o domínio para sairá de todos os valores de que gerem entre e .
Olhando no gráfico, isso acontece para e para , onde é um valor entre e . Assim, ficamos com a opção :