Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Esboço de Gráfico

Ver Teoria
Exercício 651234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636466676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Seja

f x = x l n 2 - 1 x

a) Determine o domínio da função f .

b) Determine as equações das retar assíntotas verticais do gráfico de f , caso existam.

c) Mostre que a reta y = ln ⁡ 2 x - 1 2 é assíntota oblíqua do gráfico de f para a direita (ou seja, quando x → + ∞ )

d) Sabendo que f é crescente em todo o seu domínio e que a reta y = ln ⁡ 2 x - 1 2 é assíntota obliqua do gráfico de f para os dois lados (ou seja, quando x → ∞ e x → - ∞ ), esboce abaixo o gráfico de f e suas retar assíntotas verticais, caso existam.

Passo 1

a) Sabemos inicialmente que o domínio do ln vai de zero a + ∞ , certo?

Então

2 - 1 x > 0 → 2 x x - 1 > 0 → 2 x - 1 > 0   e   x > 0 → x > 1 2 o u 2 x - 1 < 0   e   x < 0 → x < 0

Logo, o D o m f = ( - ∞ , 0 ) ∪ 1 2 ,   ∞

Passo 2

b) Para determinarmos as assíntotas verticais, os valores para onde nosso x vai tender é aquele onde a função não existe, certo? No nosso caso seriam x = 0 e x = 1 2 e precisamos encontra infinito como resultado desses limites.

lim x → 0 - ⁡ f x = lim x → 0 - ⁡ x l n 2 - 1 x

lim x → 0 - ⁡ ln ⁡ 2 - 1 x 1 x

Aplicando L’hospital

lim x → 0 - ⁡ 1 2 - 1 2 1 x 2 - 1 x 2

lim x → 0 - ⁡ - 1 2 - 1 x = 0

Opa, se não é igual a infinito, não temos uma assíntota vertical aqui.Bora tentar agora com o limite indo pra 1 2

lim x → 1 2 + ⁡ f ( x ) = lim x → 1 2 + ⁡ x l n 2 - 1 x = lim x → 1 2 + ⁡ - ∞

Agora sim!! Então temos em x = 1 2 uma assíntota vertical.

Passo 3

c) O que vamos precisar lembrar qui incialmente é que

m = lim x → ∞ ⁡ f x x → lim x → ∞ ⁡ x l n 2 - 1 x x → lim x → ∞ ⁡ ln ⁡ 2 - 1 x = l n 2

E

n = lim x → ∞ ⁡ f x - m x

= lim x → ∞ ⁡ x l n 2 - 1 x - l n 2 x

= lim x → ∞ ⁡ x ln ⁡ 2 - 1 x - l n 2

= lim x → ∞ ⁡ ln ⁡ 2 - 1 x - l n 2 1 x

Aplicando a regra de L’hospital

= lim x → ∞ ⁡ 1 2 - 1 x 1 x 2 - 1 x 2

= lim x → ∞ ⁡ - 1 2 - 1 x = - 1 2

Passo 4

d)

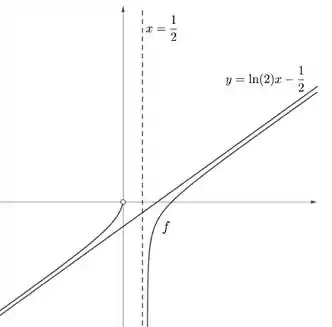
Resposta

a )   D o m f = ( - ∞ , 0 ) ∪ 1 2 ,   ∞

b )   x = 1 2

c )   - 1 2

d )  

Exercícios de Livros Relacionados

Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2