Seja a função definida por:
Obtenha, caso existam:
- As assíntotas horizontais e verticais do gráfico de .
- Os intervalos onde é crescente e onde é decrescente.
- Os intervalos onde o gráfico de é côncavo para cima, onde é côncavo para baixo e os pontos de inflexão.
Passo 1
Como sempre, obtemos as assíntotas horizontais da seguinte forma:
Reescrevendo a função para observamos melhor seu comportamento (ou você poderia “substituir” o , acho que ficaria claro):
Portanto temos uma indeterminação do tipo . Derivando por L’Hospital:
Passo 2
Portanto uma assíntota horizontal é a . Pelo outro lado teremos:
O comportamento talvez não esteja claro neste caso. Vamos fazer a mesma manipulação que fizemos no passo anterior. Só que antes, pra simplificar, vamos fazer uma mudança de variáveis:
Assim, o nosso limite fica:
Agora podemos resolver o limite. “Substituindo”, pra ver no que dá:
Portanto:
E essa outra assíntota horizontal não existe.
Passo 3
Investigando as verticais, nós percebemos que não há nenhum valor de que force uma divisão por zero ou outra atrocidade algébrica que gere uma assíntota vertical. Portanto elas não existem para esta função.
Outra maneira de dizer isso é dizendo que é contínua em ℝ.
Passo 4
Os intervalos onde é crescente respeitam a seguinte relação:
E os intervalos em que é decrescente respeitam:
Portanto, pela regra do produto:
Encontrando os intervalos em que é crescente:
Como uma exponencial é sempre positiva e diferente de zero podemos corta-la:
Pela nossa análise da tabela de sinais, temos:
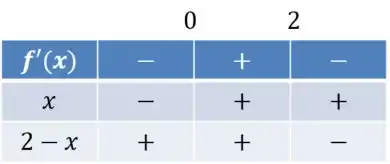
Portanto é crescente no seguinte intervalo:
E, como já concluímos toda a análise do sinal, podemos seguramente dizer que é decrescente em:
Passo 5
A mesma lógica se segue para intervalos de concavidade. Pela regra do produto, temos:
Como temos que:
Para todo o real, então esse termo não entra na nossa análise de sinais.
Analisamos então o sinal do polinômio .
Pelo teorema fundamental da álgebra, achamos as raízes do polinômio para poder reescreve-lo:
Portanto:
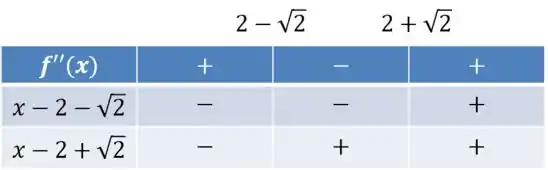 Pela análise da tabela de sinais:
Pela análise da tabela de sinais:
Temos então que a função tem concavidade para cima em:
E, analogamente, para baixo em:
Por consequência da nossa análise, sabemos que os pontos em que a derivada segunda zera (pontos de inflexão) são:
Portanto os pontos de inflexão são:
Passo 6
O esboço do gráfico é, portanto:
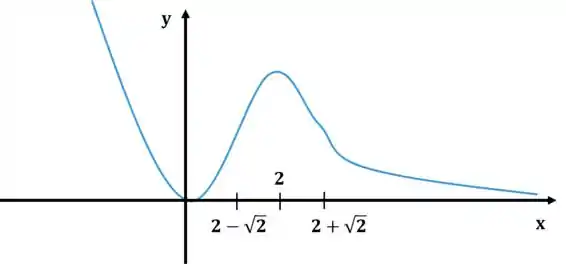
Resposta
Ei, a resposta está no passo a passo :)