2) Seja uma função duas vezes diferenciável em seu domínio tal que:
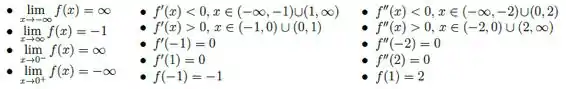
- Faça um esboço do gráfico de , indicando claramente as regiões de crescimento e decrescimento, os pontos extremos relativos, os pontos extremos absolutos, assíntotas, concavidade do gráfico e pontos de inflexão.
- A função tem quantas raízes em ? E em ? (Se não houver informação suficiente para se determinar a quantidade exata de raízes, indique quais são as quantidades possíveis). Justifique.
Passo 1
Essa questão tem uma parte boa e outra ruim. A boa é que não precisamos fazer nenhuma conta pro esboço. A ruim, é que temos que interpretar com muito cuidado tudo que nos foi dado. Vamos começar olhando pros limites:
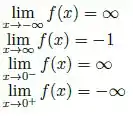
Como limites pros infinitos são o artíficio que usamos pra achar assíntotas horizontais, vamos ter assíntota horizontal só quando esses limites derem números. Nesse caso, um deles deu! Então nosso esboço, por enquanto, fica:
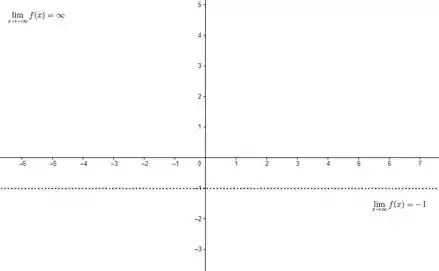
Agora, os limites laterais que fazemos pra determinado valor de são os artifícios que usamos pra encontrar assíntotas verticais. Se fizermos os limites laterais e pelo menos um deles explodir pra algum infinito, o valor de que escolhemos é uma assíntota sim! E nesse caso, os dois explodem! Então é uma assíntota vertical! Nosso esboço fica:
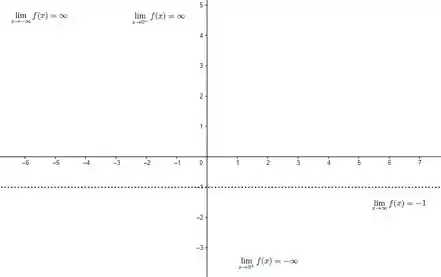
Na real por enquanto só fizemos as assíntotas. Deixamos os limites escritos só pra indicar pra onde a função vai quando tivermos desenhando ela.
Passo 2
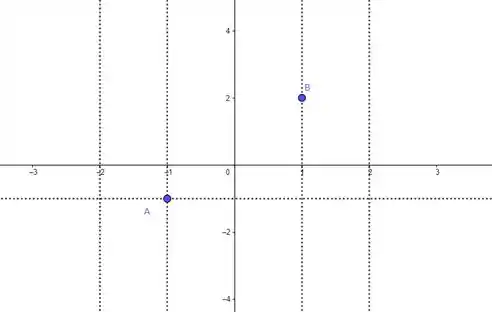
Show, vamos olhar pra todas as partes que envolvam pontos:
![]()
Pô, bora então marcar esses pontos no nosso esboço!
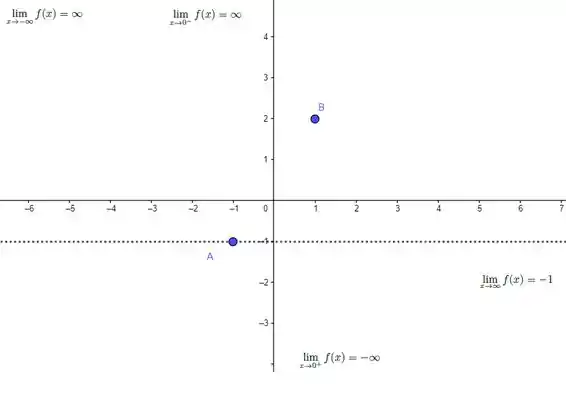
Beleza. Por enquanto não temos mais informações que deêm pra gente escrever diretamente no nosso esboço. Mas a gente pode olhar pra essas linhas aqui ó:
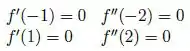
Como elas nos ajudam? Saca só, esses são os pontos que zeram a primeira e a segunda derivada, representando então as fronteiras de mudança sinal. Pras primeiras derivadas, e são fronteiras de intervalos de crescimento e descrescimento da função! Pras segundas derivadas, e são fronteiras de intervalos de concavidade pra cima e pra baixo da função (pontos de inflexão)!

Note ainda que sabemos que é uma assíntota vertical! Vamos então montar um quadrinho com esses pontos, seguindo esse estilo:
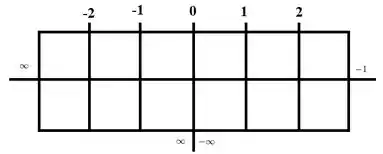
Onde:
Representa o resultado dos limites pros infinitos, ou seja, a existência ou não de assíntotas horizontais e
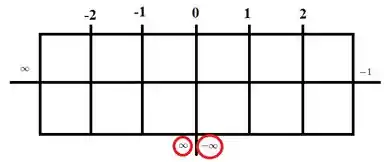
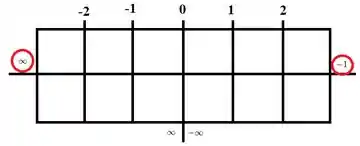
Representa o resultado dos limites laterais feitos no passo anterior, mostrando que nessa tabela é tratado como assíntota, em que a função vai pra pra valores a esquerda de e sai do pra valores a direita de . Com essa tabelinha, conseguimos analisar crescimento/decrescimento e concavidade da função em todos os intervalos mais importantes pra essa função, que são:
E pra demarcar bem esses intervalos no esboço, podemos desenhar assim:
Passo 3
Agora, pra preenchermos a tabela, tudo que precisamos é analisar bem essas linhas:
![]()
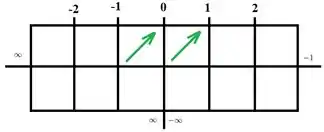
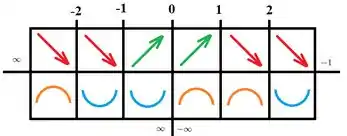
Pra primeira coluna, que fala só das primeiras derivadas, temos função crescente (primeira derivada positiva) nos intervalos e , então marcamos na nossa tabela:
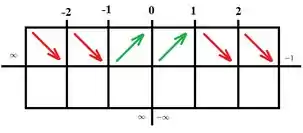
E temos função decrescente (primeira derivada negativa) no intervalo , que é a união dos intervalos e , e no intervalo , que é a união dos intervalos e . Marcamos na nossa tabelinha:
Agora, pra segunda derivada, temos que a concavidade é pra cima (segunda derivada positiva) em , que é a união dos intervalos e , e também no intervalo . Marcamos na tabelinha:
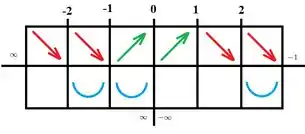
E a concavidade será pra baixo (segunda derivada negativa) nos intervalos e , que é a união dos intervalos e , fazendo a gente fechar nossa tabela:
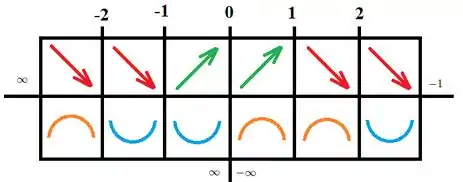
Passo 4
Agora é hora de por a mão na massa, vamos esboçar essa função usando a tabela:
Em , a função vai decrescer com a concavidade pra baixo vindo do . Um esboço bom desse pedaço seria:
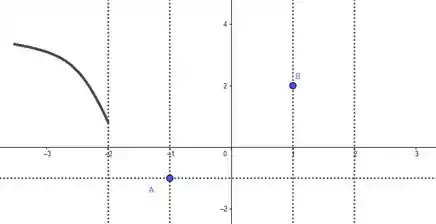
Em , a função vai decrescer com a concavidade pra cima e vai tocar no ponto . Um esboço bom desse pedaço seria:
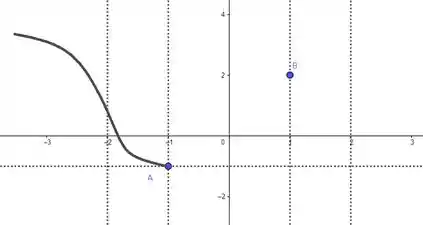
Em , a função vai crescer com a concavidade pra cima e vai até o . Um esboço bom desse pedaço seria:
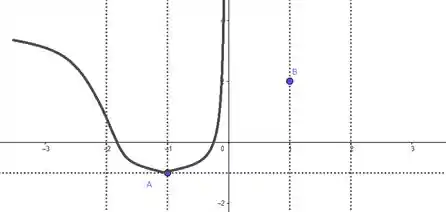
Em , a função vai crescer com a concavidade pra baixo, saindo do e tocando no ponto . Um esboço bom desse pedaço seria:
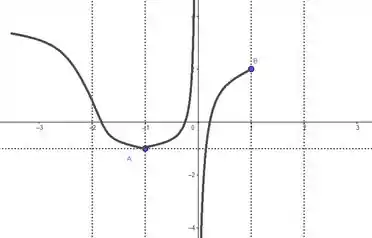
Em , a função vai decrescer com a concavidade pra baixo. Um esboço bom desse pedaço seria:
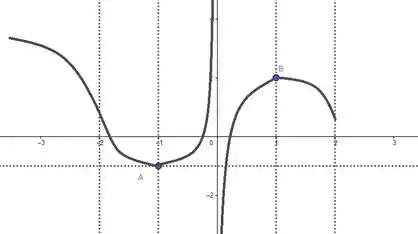
E pra fechar, em , a função vai decrescer com a concavidade pra cima, tendendo a . Um esboço bom desse pedaço seria:
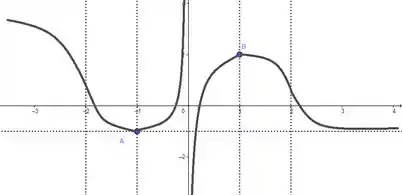
E taí! Esboço terminado!
Passo 5
Pra fechar com chave de ouro a gente precisa responder a letra , que nos pergunta: A função tem quantas raízes em ? E em ?
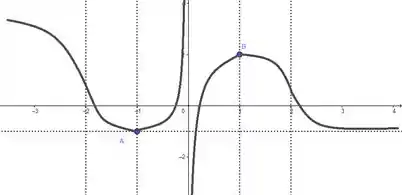
Bem, pro primeiro intervalo, a resposta é exatamente duas raízes, pois a função vem de , passa por um ponto localizado abaixo do eixo e volta pro quando . Pra isso ser possível a curva da função deve, obrigatoriamente, tocar duas vezes no eixo , marcando duas raízes.
A gente pode seguir a mesma lógica pro intervalo , obrigatoriamente temos duas raízes! E a localização de uma também é fixa, pois em a função vai de até um ponto acima do eixo , tendo que cortar ele necessariamente uma vez. Agora, a segunda raiz pode estar localizada tanto em quanto em , sendo impossível afirmar onde ela está com as informações que temos. Então em temos obrigatoriamente uma raiz, mas com a possibilidade de haverem duas.
Graficamente, o caso em que temos a segunda raiz de dentro de é exatamente idêntico ao esboço que já fizemos:
O outro caso, em que a segunda raiz de de está dentro de , seria como se tivéssemos:
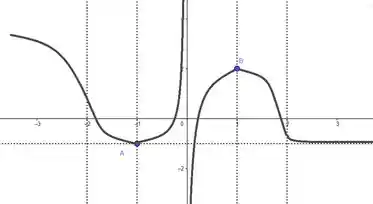
Note que esse esboço diferente não tá errado em relação a tudo que vimos nos outros passos :D
Resposta
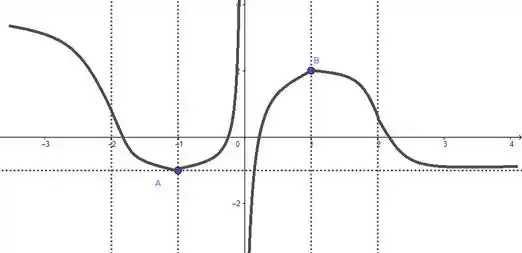
- Justificativas no Passo 5. Em temos obrigatoriamente duas raízes. Em temos obrigatoriamente uma raiz, mas podemos ter uma segunda. A localização da seguda raiz como dentro ou fora deste intervalo depende de informações sobre que não possuímos.