IME, Cálculo 1, 2019, VC, Q4
Seja ; . Prove (usando derivação) que ou prove (usando teoremas de continuidade) que existe um número , tal que
Passo 1
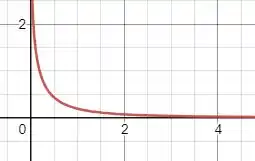
Faleis vós, ó consagrados! Antes de decidir enveredar por qualquer um dos caminhos apresentados, analisemos a função. Quando , observe que o logaritmo cresce infinitamente e a razão converge, logo . A partir daí analisemos o crescimento da função:
Logo, para tornando a função estritamente decrescente.
Passo 2
Temos ainda que:
Basta verificar se a função tende a 0 por cima ou por baixo, de forma a verificar sua positividade. Para isto, considere que:
Logo, , tal que nesse intervalo a concavidade da função está para cima e de fato a função tende a 0 superiormente, sem nunca admitir número tal que . Assim, .
Resposta
Exercícios de Livros Relacionados
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2