UFMG; Cálculo 1; Prova 2 – 2022.1; Exercício 3
3) Use o roteiro feito em aula para esboçar a curva . Indique todos os passos do roteiro, isto será tomado em conta na avaliação.
Passo 1
Saaalve, turma! Tudo certo com vocês? Estou feliz em resolver mais uma questão. Vamos pra cima!
Para começarmos a traçar o gráfico, vamos encontrar as raízes (pontos que cortam ou tocam o eixo). Para isso, vamos igualar a função a :
é uma solução!
é a única raiz real.
Portanto o gráfico tem e como raízes.
Passo 2
Agora, encontraremos o ponto de inflexão desse gráfico. Esse é o ponto que muda a concavidade (tendência) da função.
Para isso, calcularemos a segunda derivada de e igualaremos a zero.
Primeira derivada:
Segunda derivada:
Igualando a zero:
Aplicando na função original:
Passo 3
Os últimos valores que precisamos encontrar são os máximos e mínimos locais. Eles são os “limites” do eixo após a inflexão.
Para isso, faremos a primeira derivada e igualaremos a zero.
Como já conhecemos a primeira derivada;
Então:
e
Aplicando em :
Passo 4
Conhecendo todos esses pontos, fica fácil traçar o gráfico, não é?
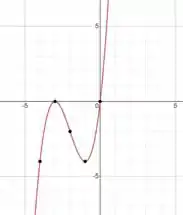
Ufa! Terminamos!
Pra essa questão é isso pessoal! Bora pra mais uma?
Resposta
Resposta no desenvolvimento do exercício.