Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Função Potencial

Ver Teoria
Exercício 411234567891011121314151617181920212223242526272829303132333435363738394042434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere o campo de forças plano:

F x ,   y = c o s   y   + y + e x ,   2 y - x   s i n   y   + x ,     x ,   y ∈ R 2

  1. Justifique, sem calcular potenciais, se o campo F é conservativo ou não.
  2. Se o campo F for conservativo, calcule seus potenciais.
  3. a > 0 . Calcule o trabalho realizado pelo campo F ao deslocar uma partícula ao longo da curva

ε = x 2 4 + y - a 2 = a 2 ,   x ≥ 1

Orientada chegando à origem.

Passo 1

  1. Pow, pela teoria sabemos que se o rotacional de um campo for 0 e esse campo estiver definido em toda região que estamos trabalhando, ou seja, se ele não tiver singularidades, ele é conservativo.

    2. Como o campo não tem singularidades basta verificar o rotacional. Bora? ☺

    Pela teoria

    r o t   F → = ∂ Q ∂ x - ∂ P ∂ y

    Onde

    F x ,   y = c o s   y   + y + e x ,   2 y - x   s i n   y   + x

    Calculando a primeira derivada parcial

    ∂ Q ∂ x = ∂ 2 y - x   s i n   y   + x ∂ x

    ∂ Q ∂ x = - s i n   y   + 1

    Calculando a segunda

    ∂ P ∂ y = ∂ c o s   y   + y + e x ∂ y

    ∂ P ∂ y = - s i n   y   + 1

    Voltando para o rotacional...

    r o t   F → = ∂ Q ∂ x - ∂ P ∂ y

    r o t   F → = - s i n   y   + 1 - - s i n   y   + 1

    r o t   F → = 0

    Logo o campo é conservativo!

    Passo 2

  2. Pois então, para calcular as funções potenciais, vamos usar uma preciosa informação, a teoria: se ω é uma função potencial de F → então F → = ∇ ω . WHAT???

    3. Calma! Esse ω aí é a função potencial, o que a gente vai fazer igualar o seu gradiente ao campo dado!☺

    ∂ ω ∂ x , ∂ ω ∂ y = c o s   y   + y + e x ,   2 y - x   s i n   y   + x

    Portanto

    I         ∂ ω ∂ x =   c o s   y   + y + e x

    I I           ∂ ω ∂ y = 2 y - x   s i n   y   + x

    Pegando a primeira

    ∂ ω ∂ x = c o s   y   + y + e x

    E integrando com relação a x , vamos obter

    ω = ∫ c o s   y   + y + e x d x

    calculando essa integral aí com relação a x (tomando y como uma constante), teremos

    ω = x   c o s   y   + x y + e x + g y

    Note que apareceu uma função que depende de y apenas, pois se derivando em relação a x ela desaparece, integrando em relação a x ela aparece. Sacou? :)

    Passo 3

    Note que já ganhamos a função potencial, porém temos ainda que ver quem essa função de y é. Para fazer isso, vamos derivar com relação à y agora e igualar com a função ( I I ) acima.

    Derivando então essa   ω = x   c o s   y   + x y + e x + g y com relação à y ...

      ∂ ω ∂ y = - x   s i n   y   + x + g ' y

    Igualando à I I       ∂ ω ∂ y = 2 y - x   s i n   y   + x

    - x   s i n   y   + x + g ' y = 2 y - x   s i n   y   + x

    Cortando esses caras e simplificando, teremos

    g ' y = 2 y

    Integrando agora com relação a y ...

    g y = ∫ 2 y d y

    g y = y 2 + c

    Note que c é a constante de integração.

    Passo 4

    Voltando para o problema inicial... As funções potenciais de F é:

    ω = x   c o s   y   + x y + e x + g y

    ω = x   c o s   y   + x y + e x + y 2 + c

    Passo 5

  3. Pow, calcular um trabalho w é, para nós na matemática, calcular uma integral de linha em cima da curva ε : w = ∫ ε   F → d r → .

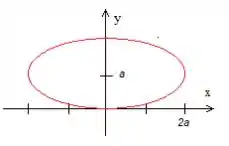
Mas quem é a curva ε ?

Então, se a gente reparar bem, essa curva é muito conhecida nossa! É uma elipse quer ver só? ☺

x 2 4 + y - a 2 = a 2

Passando esse a 2 dividindo

x 2 4 a 2 + y - a 2 a 2 = 1

x 2 2 a 2 + y - a 2 a 2 = 1

Essa equação, representa uma elipse deslocada de a unidades pra cima em y e com o eixo maior paralelo a x valendo 2 a e o eixo menor valendo apenas a e paralelo a y , dessa forma aqui

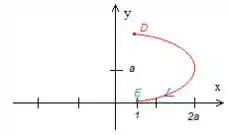
Como queremos apenas a parte onde x ≥ 1 e ela está orientada no sentido da origem, ou seja

Passo 2

Como já calculamos uma função potencial para F vamos usar esse detalhe ao invés de calcular a integral diretão ☺!

O trabalho realizado pela partícula nessa curva saindo do ponto vermelho D lá em cima e chegando no ponto verde E de baixo é dado por

w = ∫ ε   F → d r → = ω E - ω ( D )

Agora, quem são esses pontos?

Passo 3

Pois então, para determinar esses pontos vamos utilizar do fato que ambos têm a coordenada x = 1 , pois é o menor valor que x pode assumir. Logo, jogando esse detalhe na equação da elipse

x 2 4 + y - a 2 = a 2

1 2 4 + y - a 2 = a 2

Passando esse 1 4 pro outro lado

y - a 2 = a 2 - 1 4

extraindo a raiz

y - a = ± a 2 - 1 4

E por fim jogando o a pro outro lado, teremos

y = a ± a 2 - 1 4

Observe que o pedaço positivo é do ponto maior, enquanto o ramo negativo do ponto mais embaixo E .

Logos os pontos têm coordenadas

D = 1 ,   a + a 2 - 1 4

E = 1 ,   a - a 2 - 1 4

Passo 4

Voltando para o cálculo do potencial

w = ∫ ε   F → d r → = ω E - ω ( D )

Onde a função potencial é ω = x   c o s   y   + x y + e x + y 2 , mas enfim, substituindo as coordenadas já encontradas, vamos obter

Para ω E

ω E = ω 1 ,   a - a 2 - 1 4 =

= c o s   a - a 2 - 1 4   + a - a 2 - 1 4 + e 1 + a - a 2 - 1 4 2 =

Resolvendo esses caras

=   c o s   a - a 2 - 1 4   + a - a 2 - 1 4 + e + a 2 - 2 a a 2 - 1 4 + a 2 - 1 4 2

Para ω D

ω D = ω 1 ,   a + a 2 - 1 4

= c o s     a + a 2 - 1 4   + a + a 2 - 1 4 + e +   a + a 2 - 1 4 2

= c o s     a + a 2 - 1 4   + a + a 2 - 1 4 + e + a 2 + 2 a a 2 - 1 4 + a 2 - 1 4 2

Quando a gente fizer a subtração desses dois caras ω E - ω ( D ) , muitos termos desses vão se cortar, ficando, portanto

W = ω E - ω D = c o s c o s   a - a 2 - 1 4   - c o s c o s   a + a 2 - 1 4   - 6 a a 2 - 1 4

Resposta

  1. Conservativo
  2. ω = x   c o s   y   + x y + e x + y 2 + c
  3. W = c o s   a - a 2 - 1 4   -   c o s   a + a 2 - 1 4   - 6 a a 2 - 1 4

Exercícios de Livros Relacionados

6. Mostre que as integrais ∮ C F 1 x , y d x + F 2 x , y d y São nulas, quais quer que sejam os contornos fechados C contidos no domínio F 1,F 2 , onde F 1 x , y = sen ⁡ x + 4 x y F 2 x , y = 2 x 2 -
Um escoamento é representado pelo campo de velocidade v → = y 2 + z 2 i → + x z j → + 2 x 2 y 2 k → Verificar se o escoamento é:b) irrotacional.
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?f) f → x , y , = x 2 + y , y 2 - x , em R 2
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?g) f → x , y , z = - sen ⁡ x + cos ⁡ x , z , y em R 3
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?h) f → x , y , = sen ⁡ x , cos ⁡ y , em R 2