Determine o trabalho realizado pelo campo de força
ao se mover uma partícula ao longo da curva , dada por , para , mostrada abaixo.
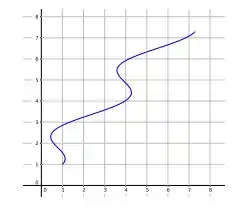
Passo 1
Então, aqui a primeira coisa que devemos fazer é nos perguntar: qual método de resolução irá nos ajudar?
Bem, como o campo não é nada fácil e a curva menos ainda, com certeza nós não vamos resolver isso aí direto.
O que a gente já sabe é que se o campo tiver potencial, o problema fica fácil!
Então bora ver se isso realmente acontece aí?
Passo 2
Bem, um campo só tem potencial se ele não tiver problema onde estivermos trabalhando.
E isso acontece, pois o campo tem problema no e no (divisão por zero na função ). Mas... o curva azul nem chega perto dessa retinhas, percebeu :D
A outra condição é o rotacional ser , se lembra?!
Então calculando esses caras, lembrando que
ou seja, a é a primeira e é a segunda entrada....
Derivando...
Calculando a outra derivada
Epa! Se fizermos
Corta, corta e realmente zera!
Isso quer dizer que o campo tem função potencial que simplifica a nossa vida, bora encontra-lo?
Passo 3
Ok! Aqui devemos lembrar-nos da teoria, beleza?
Se ele é conservativo então ele satisfaz . Mas quem é esse ômega que apareceu aí? :\
Esse ômega é a função potencial, e pela teoria o gradiente dela deve ser igual ao campo , só isso, beleza?
Portanto a gente pode dizer que
Passo 4
Então o que a gente deve fazer agora é pegar a primeira integrar com relação a
Note que aparece um aí, pois se derivarmos em relação a ela some, então integramos ela volta. Mas não se preocupe, no próximo passo determinamos ela
A integral das somas é a soma das integrais...
Integrando em (portanto é uma constante)
Passo 5
Como eu disse, vamos agora determinar , e como podemos fazer isso?
Derivando com relação a e depois comparando com o que temos em ...
Comparando agora com o que temos em do passo 3...
Cortando essas coisas iguais
Integrando dos dois lados
Tomando essa constante como zero (ela é indiferente pra nós aqui ), uma função potencial para a é
Passo 6
Pela teoria, se é uma função potencial para , então
Onde é o ponto final e é o de inicio. No nosso caso esses pontos são obtidos nos limites da curva, portanto o ponto , é quando
Logo
E quanto ao , é quando
Como as coordenadas são iguais, como ao , ele vai zerar também, portanto