Considere a hélice com
(1.1) Determine os pontos e em que a hélice acima encontra a esfera de equação
(1.2) Calcule o comprimento de arco da hélice ligando a
(1.3) Calcule a integral de linha do campo ao longo do arco ligando a .
Passo 1
Para determinarmos esses pontos é BEM tranquilo! Vamos simplesmente substituir os valores de e da parametrização da hélice dentro da equação da esfera.
Vamos lembrar da relação trigonométrica que
Logo
Perfeito, sabemos que os pontos de interseção vao ser então
Passo 2
Vamos partir agora para o comprimento do arco. Lembra que pra isso temos uma formulinha?
Lembrando que
Trazendo de volta pra integral
Passo 3
Por último mas não menos importante, vamos começar essa última questã aí. Acredito que você concorde comigo que método direto ai seria bem complicado, não?
Minha dica aqui é calcularmos o rotacional desse campo. Se ele for igual a zero, sabemos que temos um campo conservativo, oq eu nos permite usar a função petencial, que ajuda muito nossa vida! Pra calcularmos o rotacional, vamos lembrar que
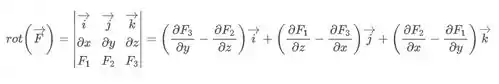
Onde o campo é
Opa, se nosso rotacional é zero, sabemos que nosso campo é conservativo! Maravilha
Passo 4
Podemos então calcular o
Vamos então calcular
Temos entçao que
Então nosso
Passo 5
Vamos voltar pra nossa parametrização
Sustituindo na função potencial
Sabemos que o cosseno de um número, e o cosseno desse número negativo, temo o mesmo valor, ou seja
Já para o seno, temos valores opostos, ou seja
Tendo isso em menta fazemos