Questão 5:
- Encontre constantes e tais que a integral
- Para os valores de e encontrados acima, calcule a integral do item onde é o semicírculo com , orientada no sentido horário.
não dependa do caminho de integração.
Passo 1
Letra a:
Para que a integral não dependa do caminho, o campo tem que ser conservativo. De acordo com a teoria, um campo é conservativo quando:
- É irrotacional.
- O domínio deve ser simplesmente conexo.
No nosso caso, o campo possui todo o como um domínio simplesmente conexo, já que e são números e é formado apenas por expressões que “funcionam” bem qualquer ponto do plano:
Para verificá-la se ele é irrotacional, basta então verificar:
Como e , então temos que:
Para essa expressão ser , considerando que e , não são :
Logo...
Para esses únicos valores, é de fato conservativo, ou seja, independe do caminho!
Passo 2
Letra b:
Poxa, já que sabemos que o campo independe do caminho, podemos tirar isso como vantagem para resolver essa letra, não é? SIM!
De acordo com a teoria de campos conservativos, podemos calcular uma integral de linha assim:
Onde é uma função potencial para o campo ; e são os pontos de início e fim da curva que estamos trabalhando. Então, veja que temos que encontrar esses caras, e a partir daí é só jogar nessa igualdade. Vamos nessa?
Passo 3
Primeiro vamos encontrar a função potencial da seguinte forma:
Onde é o gradiente:
Logo, com o campo :
Logo:
Vamos utilizar essas equações para extrair . Então partiu!
Passo 4
Primeiro vamos usar a primeira equação diferencial para encontrar :
“Passando” o para o outro lado e integrando:
Integrando então com relação a , então considerando constante...
Essa é uma constante de integração, mas ela é uma constante apenas em relação , pois em relação à ela é uma função ainda. Faz sentido ela aparecer, pois se você derivar novamente essa função com relação , a derivada dessa função desaparece, então na integral ela ressurge, saca?
Veja então que a gente já descobriu quem é a função potencial . Basta mesmo saber quem é essa função ...
Passo 5
Para encontrar tal função, vamos derivar essa função aí com relação a e comparar com a equação diferencial numero (). Então derivando...
Comparando essa equação com o que temos em ...
Tiramos que...
Para isso ser verdade, então é uma constante qualquer :
Pois, a derivada de uma constante é sempre . Bem, temos então a nossa função potencial:
Passo 6
Para encontrar o valor da integral, então, precisamos agora dos pontos e . Para isso, devemos nos atentar de que queremos encontrar a integral em cima de definida por: com orientada no sentido horário. Se a gente desenhar essa curva...
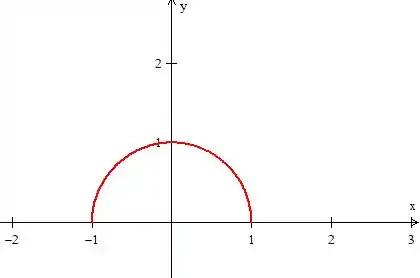
Veja que o ponto o ponto inicial dela é enquanto que o ponto final .
Passo 7
Com tudo encontrado então, podemos calcular a integral:
Calculando ...
Enquanto que ...
Logo:
Resposta
Letra ) ,
Letra )