Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Função Potencial

Ver Teoria
Exercício 301234567891011121314151617181920212223242526272829313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Seja C o trecho da parábola 2 y = - 2 x 2 + x + 1 de (-1, -1) a (1,0). A integral ∫ C - y x 2 + y 2 d x + x x 2 + y 2 d y   é igual a:

Passo 1

Logo de cara a gente consegue perceber que resolver isso daí pelo método direto ia ser bem complicado. Joga a parametrização disso aí dentro dessa campo não ia ser maneiro.

Vamos ver se nosso r o t F = 0 , o que seria um facilitador na nossa vida.

r o t F = ∂ F 2 ∂ x - ∂ F 1 ∂ y

∂ F 2 ∂ x = x 2 + y 2 - 2 x 2 x 2 + y 2 2

∂ F 1 ∂ y = - x 2 + y 2 + 2 y 2 x 2 + y 2 2

Logo:

r o t F = 0

Passo 2

Opa, isso pode ser um grande facilitador na nossa vida. Lembra que quando estamos trabalhando com um campo conservativo temos a independência do caminho?

Fazer a integral de linha em cima dessa curva:

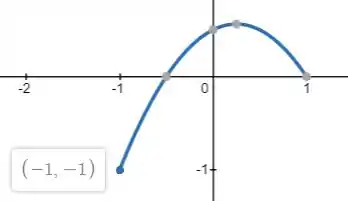
Expressa o mesmo resultado numérico dessa abaixo:

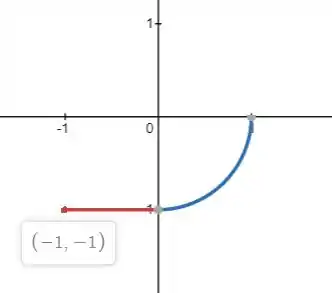
No entanto, perceba que na segunda imagem estamos trabalhando com duas curvas. Então ficamos com:

∫ C F   d r =   ∫ r F   d r   + ∫ C 1 F   d r

Onde r representa a reta vermelha, e C 1 representa a semi circunferência azul.

Passo 3

Calculando a integral de linha em cima da reta temos:

Parametrizando a reta:

r t = t , - 1

- 1 ≤ t ≤ 0

Termo ds:

r ' t = ( 1,0 )

Não podemos esquecer de escrever o campo em função da parametrização.

F = - y x 2 + y 2 , x x 2 + y 2

F r t = 1 t 2 + 1 , t t 2 + 1

Montando então nossa integral ficamos com:

∫ - 1 0 1 t 2 + 1 , t t 2 + 1 1,0 d t

∫ - 1 0 1 t 2 + 1 d t

a r c t g 0 - a r c t g ( - 1 )

0 - - π 4

= π 4

Passo 4

Bom, até então calculamos a integral em cima da reta, ficamos ainda faltando a integral em cima do semi circulo que varia entre 3 π 2 até 2 π .

Parametrizando:

φ t = cos ⁡ t ,   s e n t

3 π 2 ≤ t ≤ 2 π

Termo ds:

φ ' t = - s e n ( t ) ,   c o s ⁡ ( t )

Escrevendo o campo em função da parametrização ficamos com:

F = - y x 2 + y 2 , x x 2 + y 2

F φ t = - s e n ( t ) , c o s ⁡ ( t )

Montando a integral e resolvendo:

∫ 3 π 2 2 π - s e n t , cos ⁡ t - s e n t , cos ⁡ t d t

∫ 3 π 2 2 π s e n 2 t + cos 2 ⁡ ( t ) d t

∫ 3 π 2 2 π 1 d t

= 2 π - 3 π 2

= π 2

Passo 5

Pra finalizar então voltamos a nossa igualdade:

∫ C F   d r =   ∫ r F   d r   + ∫ C 1 F   d r

∫ C F   d r =   π 4 + π 2

= 3 π 4

Resposta

= 3 π 4

Exercícios de Livros Relacionados

6. Mostre que as integrais ∮ C F 1 x , y d x + F 2 x , y d y São nulas, quais quer que sejam os contornos fechados C contidos no domínio F 1,F 2 , onde F 1 x , y = sen ⁡ x + 4 x y F 2 x , y = 2 x 2 -
Um escoamento é representado pelo campo de velocidade v → = y 2 + z 2 i → + x z j → + 2 x 2 y 2 k → Verificar se o escoamento é:b) irrotacional.
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?f) f → x , y , = x 2 + y , y 2 - x , em R 2
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?g) f → x , y , z = - sen ⁡ x + cos ⁡ x , z , y em R 3
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?h) f → x , y , = sen ⁡ x , cos ⁡ y , em R 2