Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Função Potencial

Ver Teoria
Exercício 521234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 2:

Seja o campo

F x ,   y = 2 x y + 1 x + 2 x y 2 1 + x 2 y 2 ,   x 2 + 2 x 2 y 1 + x 2 y 2

  1. Justifique se F é conservativo ou não sem calcular potenciais.
  2. Caso F ser conservativo, calcule os potenciais para F .
  3. Seja o campo

G x ,   y = 2 x y + 1 x + 2 x y 2 1 + x 2 y 2 + x y ,   x 2 + 2 x 2 y 1 + x 2 y 2 + x sin ⁡ π x y ,     x > 0

Calcule ∫ C   G d r onde C é o segmento de 1 ,   - 1 até 1 ,   1 .

Passo 1

a )

Pow, pela teoria sabemos que se o rotacional de um campo for 0 e esse campo estiver definido em toda região que estamos trabalhando, ou seja, se ele não tiver singularidades, ele é conservativo.

Vamos averiguar primeiro o rotacional...

r o t   F → = ∂ Q ∂ x - ∂ P ∂ y

Onde

F x ,   y = 2 x y + 1 x + 2 x y 2 1 + x 2 y 2 ⏟ P ,   x 2 + 2 x 2 y 1 + x 2 y 2 ⏟ Q

Calculando a primeira derivada parcial

∂ Q ∂ x = ∂ x 2 + 2 x 2 y 1 + x 2 y 2 ∂ x     →

∂ Q ∂ x = 2 x + ∂ ∂ x 2 x 2 y 1 + x 2 y 2     →

Atenção na regra da fração...

∂ Q ∂ x = 2 x + 1 + x 2 y 2 ⋅ ∂ ∂ x 2 x 2 y - 2 x 2 y ⋅ ∂ ∂ x 1 + x 2 y 2 1 + x 2 y 2 2       →

∂ Q ∂ x = 2 x + 4 x y 1 + x 2 y 2 - 2 x y 2 2 x 2 y 1 + x 2 y 2 2       →

∂ Q ∂ x = 2 x + 4 x y + 4 x 3 y 3 - 4 x 3 y 3 1 + x 2 y 2 2       →

∂ Q ∂ x = 2 x + 4 x y 1 + x 2 y 2 2  

Calculando a segunda

∂ P ∂ y = ∂ 2 x y + 1 x + 2 x y 2 1 + x 2 y 2 ∂ y     →

∂ P ∂ y = 2 x + ∂ ∂ y 2 x y 2 1 + x 2 y 2     →

Olha a regra da fração novamente...

∂ P ∂ y = 2 x + 1 + x 2 y 2 ⋅ ∂ ∂ y 2 x y 2 - 2 x y 2 ⋅ ∂ ∂ y 1 + x 2 y 2 1 + x 2 y 2 2     →

∂ P ∂ y = 2 x + 4 x y 1 + x 2 y 2 - 2 x 2 y 2 x y 2 1 + x 2 y 2 2     →

∂ P ∂ y = 2 x + 4 x y 1 + x 2 y 2 - 4 x 3 y 3 1 + x 2 y 2 2     →

∂ P ∂ y = 2 x + 4 x y + 4 x 3 y 3 - 4 x 3 y 3 1 + x 2 y 2 2     →

∂ P ∂ y = 2 x + 4 x y 1 + x 2 y 2 2  

Voltando para o rotacional...

r o t   F → = ∂ Q ∂ x - ∂ P ∂ y

r o t   F → = 2 x + 4 x y 1 + x 2 y 2 2 - 2 x + 4 x y 1 + x 2 y 2 2

r o t   F → = 0

Rotacional nulo e com o campo sem singularidades...

F x ,   y = 2 x y + 1 x + 2 x y 2 1 + x 2 y 2 ,   x 2 + 2 x 2 y 1 + x 2 y 2

Para x ≠ 0 , o campo torna-se conservativo. :D

Passo 2

b )

Pois então, para calcular as funções potenciais, vamos usar uma preciosa informação, a teoria: se ω é uma função potencial de F → então F → = ∇ ω . WHAT???

Calma! Esse ω aí é a função potencial, o que a gente vai fazer igualar o seu gradiente ao campo dado!

∂ ω ∂ x , ∂ ω ∂ y = 2 x y + 1 x + 2 x y 2 1 + x 2 y 2 ,   x 2 + 2 x 2 y 1 + x 2 y 2

Portanto

I         ∂ ω ∂ x = 2 x y + 1 x + 2 x y 2 1 + x 2 y 2

I I           ∂ ω ∂ y = x 2 + 2 x 2 y 1 + x 2 y 2                          

Passo 3

Pegando a segunda, já que está mais fácil...

∂ ω ∂ y = x 2 + 2 x 2 y 1 + x 2 y 2

E integrando com relação a y , vamos obter

ω = ∫ x 2 + 2 x 2 y 1 + x 2 y 2 d y + g x

Note que apareceu uma função que depende de x apenas, pois se derivando em relação a y ela desaparece, integrando em relação a x ela aparece. Sacou? :)

calculando essa integral aí com relação a y (tomando x como uma constante), teremos

ω = ∫ x 2 d y + ∫ 2 x 2 y 1 + x 2 y 2 d y + g x     →

ω = x 2 y + ∫ 2 x 2 y 1 + x 2 y 2 d y + g x     →

Essa outra integral, sai com uma substituição...

1 + x 2 y 2 = a   →

d a = 2 x 2 y   d y

ω = x 2 y + ∫ 1 a d a + g x     →

ω = x 2 y + ln ⁡ a + g x     →

Voltando para a variável...

ω = x 2 y + ln ⁡ 1 + x 2 y 2 + g x

Passo 4

Note que já ganhamos a função potencial, porém temos ainda que ver quem essa função de x é. Para fazer isso, vamos derivar com relação à y agora e igualar com a função ( I I ) acima.

Derivando então essa   ω = x 2 y + ln ⁡ 1 + x 2 y 2 + g x com relação à x ..

  ∂ ω ∂ x = ∂ ∂ x x 2 y + ln ⁡ 1 + x 2 y 2 + g x   →

∂ ω ∂ x = ∂ ∂ x x 2 y + ∂ ∂ x ln ⁡ 1 + x 2 y 2 + ∂ ∂ x g x   →

∂ ω ∂ x = 2 x y + ∂ ∂ x ln ⁡ 1 + x 2 y 2 + ∂ ∂ x g x   →

Calculando essa segunda derivada aplicando a regra da cadeia...

∂ ω ∂ x = 2 x y + 1 1 + x 2 y 2 ⋅ ∂ ∂ x 1 + x 2 y 2 + ∂ ∂ x g x   →

∂ ω ∂ x = 2 x y + 2 x y 2 1 + x 2 y 2 + ∂ ∂ x g x   →

Essa última derivada, como g é uma função que depende só de x , essa derivada vira uma derivada simples...

∂ ω ∂ x = 2 x y + 2 x y 2 1 + x 2 y 2 + g ' x

Igualando à I           ∂ ω ∂ x = 2 x y + 1 x + 2 x y 2 1 + x 2 y 2

2 x y + 2 x y 2 1 + x 2 y 2 + g ' x =     2 x y + 1 x + 2 x y 2 1 + x 2 y 2

Cortando esses caras e simplificando, teremos

g ' x = 1 x

Integrando agora com relação a y ...

g x = ∫ 1 x   d x

g x = ln ⁡ x + c

Note que c é a constante de integração, mas que poderemos considerar 0 , já que o problema nos pediu apenas uma função potêncial...

g x = ln ⁡ x

Passo 5

Voltando para o problema inicial... Uma função potencial de F é

ω = x 2 y + ln ⁡ 1 + x 2 y 2 + g x

ω = x 2 y + ln ⁡ 1 + x 2 y 2 + ln ⁡ x

Passo 6

c )

O problema agora nos pede para calcular a integral de linha...

∫ C   G d r

Onde o G é o campo...

G x ,   y = 2 x y + 1 x + 2 x y 2 1 + x 2 y 2 + x y ,   x 2 + 2 x 2 y 1 + x 2 y 2 + x sin ⁡ π x y ,     x > 0

Note que podemos separar esse campo aí em uma soma de dois outros...

G x ,   y = 2 x y + 1 x + 2 x y 2 1 + x 2 y 2 ,   x 2 + 2 x 2 y 1 + x 2 y 2 + x y ,   x sin ⁡ π x y

Ou seja, se chamarmos H x ,   y = x y ,   x sin ⁡ π x y ...

G x , y = F x ,   y + H x ,   y

O bom de fazer isso é que já calculamos uma função potencial para F e isso vai facilitar. Veja...

Passo 7

Como queremos uma integral de linha para G em cima do segmento C ...

∫ C   G x ,   y d r = ∫ C   F x ,   y d r + ∫ C   H x ,   y d r

Para a integral de linha em cima de F se calcula muito fácil, afinal de contas, temos a função potencial dele, informações do ponto de saída

A = 1 ,   - 1

e do ponto de chegada

B = 1 ,   1

Então...

∫ C   F x ,   y d r = ω B - ω A

Então...

ω = x 2 y + ln ⁡ 1 + x 2 y 2 + ln ⁡ x       →           ω B = 1 2 1 + ln ⁡ 1 + 1 2 1 2 + ln ⁡ 1   →

ω B = 1 + ln ⁡ 2

Enquanto que...

ω = x 2 y + ln ⁡ 1 + x 2 y 2 + ln ⁡ x       →           ω A = 1 2 - 1 + ln ⁡ 1 + 1 2 - 1 2 + ln ⁡ 1   →

ω A = - 1 + ln ⁡ 2

Logo...

∫ C   F x ,   y d r = ω B - ω A = 1 + ln ⁡ 2 - - 1 + ln ⁡ 2 =

2

Passo 8

Bem, mas ainda nos falta encontrar

∫ C   H x ,   y d r

E aqui não tem jeito. Temos que calcular essa integral de linha direta:

1º - Parametrizando a curva C .

2º - Encontrando o termo d r .

3º - Substituindo a parametrização no campo H .

Passo 9

Para parametrizar a curva C , vamos desenha-la... Sabemos que ela é um segmento de reta que une o ponto 1 ,   - 1 e 1 ,   1 ...

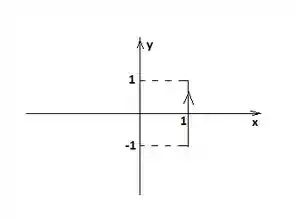
Epa! É um segmento paralelo ao eixo y passando por x = 1 ...

x = 1         e           y = t

Então...

γ t = 1 ,   t

Como y é t e y varia de - 1 a 1 , então...

- 1 ≤ t ≤ 1

Passo 10

Encontrando o termo d r ...

d r = γ ' t d t

d r = 0 ,   1 d t

E substituindo os termos da parametrização no campo...

H x ,   y = x y ,   x sin ⁡ π x y

H γ t = t ,   sin ⁡ π t

Voltando para a integral de linha...

∫ C   H x ,   y d r = ∫ - 1 1 t ,   sin ⁡ π t ⋅ 0 ,   1 d t =

∫ - 1 1 sin ⁡ π t d t =

Agora é só calcular essa integral aí ;)

∫ - 1 1 sin ⁡ π t d t = - cos ⁡ π t π - 1 1 =

- cos ⁡ π π - - cos ⁡ - π π = 1 π - 1 π =

0

Passo 11

Voltando então para a integral de linha principal que queríamos calcular...

∫ C   G x ,   y d r = ∫ C   F x ,   y d r + ∫ C   H x ,   y d r

E substituindo...

∫ C   G x ,   y d r = 2 + 0 =

2

Resposta

a )

O campo é conservativo.

b )     ω = x 2 y + ln ⁡ 1 + x 2 y 2 + ln ⁡ x

c )     2

Exercícios de Livros Relacionados

6. Mostre que as integrais ∮ C F 1 x , y d x + F 2 x , y d y São nulas, quais quer que sejam os contornos fechados C contidos no domínio F 1,F 2 , onde F 1 x , y = sen ⁡ x + 4 x y F 2 x , y = 2 x 2 -
Um escoamento é representado pelo campo de velocidade v → = y 2 + z 2 i → + x z j → + 2 x 2 y 2 k → Verificar se o escoamento é:b) irrotacional.
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?f) f → x , y , = x 2 + y , y 2 - x , em R 2
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?g) f → x , y , z = - sen ⁡ x + cos ⁡ x , z , y em R 3
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?h) f → x , y , = sen ⁡ x , cos ⁡ y , em R 2