Listas FUV - GRADMAT de Funções de uma Variável da UFABC - Lista 8 - Aplicações de Integral
Funções de uma Variável - UFABC
Encontre o volume do sólido que permanece depois que um furo circular de um raio é perfurado através do centro de um esfera sólida de raio por:
- Seções transversais
Encontre o volume do sólido que permanece depois que um furo circular de um raio é perfurado através do centro de uma esfera sólida de raio por:
b) Cascas cilindricas
Ver solução completaDeduza a fórmula do volume do toro obtido ao giramos o circulo em torno do eixo x
Ver solução completaCalcule o trabalho realizado pela força F(x) quando a partícula se desloca de até b:
- de até
Calcule o trabalho realizado pela força F(x) quando a partícula se desloca de até b:
b) de até
Ver solução completaCalcule o trabalho realizado pela força F(x) quando a partícula se desloca de até b:
c) de até
Ver solução completaCalcule o trabalho realizado pela força F(x) quando a partícula se desloca de até b:
d) de até
Ver solução completaCalcule o trabalho realizado pela força F(x) quando a partícula se desloca de até b:
e) de até
Ver solução completaSobre uma partícula que se desloca sobre o eixo x atua uma força de intensidade 3x e que forma com o eixo x um ângulo de 30°
Calcule o trabalho realizado de ao deslocar a partícula até
Ver solução completaSobre uma partícula que se desloca sobre o eixo x atua uma força sempre dirigida para o ponto P e cuja intensidade é igual ao inverso do quadrado da distância da partícula P
Calcule o trabalho realizado por ao deslocar a particular de até
Ver solução completaUma carga elétrica Q uniformemente distribuía ao longo de um condutor em forma de anel de raio a repele uma carga q como ao longo da linha perpendicular
]à plano do anel, através do seu centro. A magnitude da força que atua sobre a carga q quando está no ponto x é dado por
E a força aruá na direção do eixo x positivo. Encontre o trabalho realizado pela força de repulsão em mover a carga q de x=a até x=b
Ver solução completaUma partícula se move ao longo do eixo x com uma função velocidade . Qual a distância percorrida pela partícula entre e
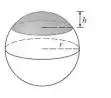
Ver solução completaUm tanque como o da figura baixo está cheio de água. Encontre o trabalho necessário para bombear todo o líquido a um nível de 1 metro acima do topo do tanque
Ver solução completaUm balde de furado, é levantado do chão até uma altura de 12m a uma velocidade constate, por uma corda que pesa . Inicialmente o balde contém de agua, mas a agua vaza a uma taxa constante e o balde acaba vazio exatamente quando atinge a altura de 12m. Quanto trabalho foi realizado?
Ver solução completaUm tanque de armazenamento de gasolina em forma de cilindro direito de raio 3 metros e comprimento de 12 metros está enterrado em solo em posição horizontal. Se topo do tanque estiver 4 metros abaixo da superfície, encontre o trabalho necessário para esvaziar um tanque cheio de gasolina pesando bombeando-o através de um tubo que se estende a uma altura de 2 metros acima do chão.
Ver solução completaEncontre a massa eo centroide das laminas abaixo
- A lamina delimitada pelo eixo x, a reta e acurva e de densidade
Encontre a massa e o centroide das lâminas abaixo:
b) a lâmina delimitada pelo eixo, a reta e a curva e de densidade
Ver solução completaEncontre a massa e o centroide das lâminas abaixo:
c) A lâmina delimitada pelo eixo , e a curva e de densidade
Ver solução completaEncontre o comprimento do arco do gráfico da equação dada entre os ponto P e Q ou no intervalo especificado.
a)
Ver solução completaEncontre o comprimento do arco do gráfico da equação dada entre os ponto P e Q ou no intervalo especificado.
b)
Ver solução completaEncontre o comprimento do arco do gráfico da equação dada entre os pontos P e Q ou no intervalo especificado.
c)
Ver solução completaEncontre o comprimento do arco do gráfico da equação dada entre os pontos P e Q ou no intervalo especificado.
d)
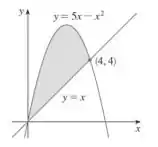
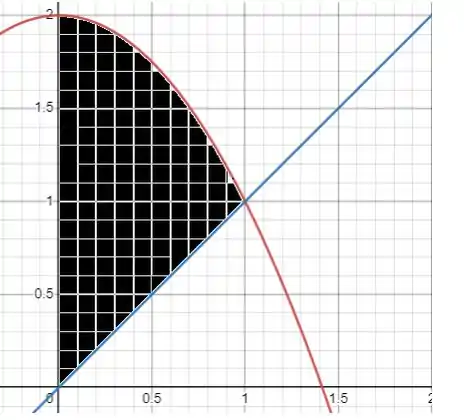
Ver solução completa2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
a) , , ,
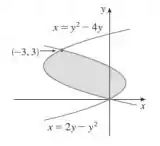
Ver solução completa2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
b)
Ver solução completa2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
c)
Ver solução completa2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
d)
Ver solução completa2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
e)
Ver solução completa2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
f)
Ver solução completaEsboce a região delimitada pelas curvas e decida se a integração deve ser feito com relação a variável x ou y. Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área de integração.
g)
Ver solução completaEsboce a região delimitada pelas curvas e decida se a integração deve ser feito com relação a variável x ou y. Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área de integração.
h)
Ver solução completaEsboce a região delimitada pelas curvas e decida se a integração deve ser feito com relação a variável x ou y. Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área de integração.
I)e
Ver solução completaAche a região delimitada pela parábola a reta tangente a está parábola no ponto (1,1) e o eixo x
Ver solução completaAche o núumero b tal que a reta divida a região delimitada pelas curvas e em duas regiões de áreas iguais.
Ver solução completaDada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
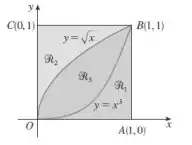
- ao longo de AO.
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
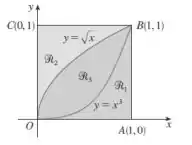
- ao longo de OC
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
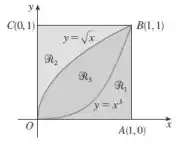
- ao longo de AB.
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
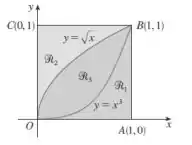
- ao longo de BC
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
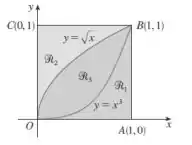
- ao longo de OA
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
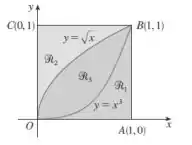
- ao longo de OC
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
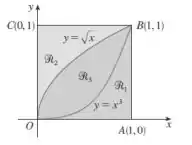
- ao longo de AB
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
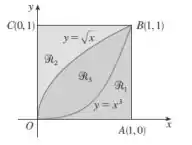
- ao longo de OA
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
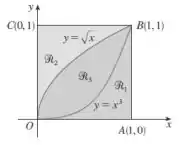
- ao longo de OC
Determine o volume dos sólidos S, usando integração.
- Um cone circular reto de altura h e base r
Determine o volume dos sólidos S, usando integração.
b) um cone truncado de base circular.

Determine o volume dos sólidos S, usando integração.
e) a região delimitada por dois cilindros circulares retos que se interceptam perpendicularmente.
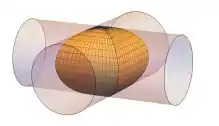
Ache o volume comum a duas esferas de raio r se o centro de cada esfera está na superfície da outra.
Ver solução completaUse o método das cascas cilíndricas para encontrar o volume da região gerada pela rotação em torno do eixo y da região delimitada pelas curvas abaixo:
Use o método das cascas cilíndricas para encontrar o volume da região gerada pela rotação em torno do eixo y da região delimitada pelas curvas abaixo:
b)
Ver solução completaUse o método das cascas cilíndricas para encontrar o volume da região gerada pela rotação em torno do eixo y da região delimitada pelas curvas abaixo:
c)
Ver solução completa