Lista 8 – Sem campus – Calculo – Funções de uma variável – Lista FUV-MADMAT – questão 2 item i
Esboce a região delimitada pelas curvas e decida se a integração deve ser feito com relação a variável x ou y. Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área de integração.
I)e
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão.
Seguinte... Temos, das funções dadas, o seguinte gráfico.
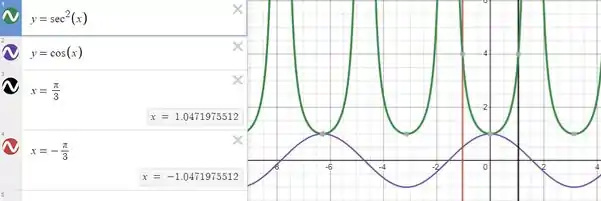
É notável que seria muito mais fácil se fizéssemos a integração com respeito ao eixo x né?! Se não fosse assim teríamos que trocar a função pro eixo y, redefinir os limites e aquela bagunça toda...
Bora pro próximo passo?
Passo 2
Obrigado por vir
Veja que a função é simétrica dos dois lados, então para acharmos o valor total da área basta acharmos a área de um lado e multiplicarmos por 2, certo?!
Sendo assim, veja que a regiçao é limitada superior e inferiormente por funções. Bom, como já sabemos então, a formula de integração desse tipo é:
Os índices s e i significam superior e inferior, respectivamente.
Passo 3
A variável x varia de 0 até que é quando as curvas se igualam a reta
Assim, já aplicando a multiplicação por 2:
Resposta
O gráfico das funções está no passo 1.
A variável é x, e dita o porquê no passo 1.
A área é: