Lista 8 – Sem campus – Calculo – Funções de uma variável – Lista FUV-MADMAT – questão 3
Ache a região delimitada pela parábola a reta tangente a está parábola no ponto (1,1) e o eixo x
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão
Antes de tudo, temos que a reta é tangente a parábola, assim:
Se ponto (1,1) então:
E assim podemos fazer nosso gráfico e achar a área, certo?!
E devemos observar bem o gráfico para sabermos como proceder com a integração. Veja!
Bora pro próximo passo?
Passo 2
Obrigado por vir.
Fazendo o gráfico, temos:
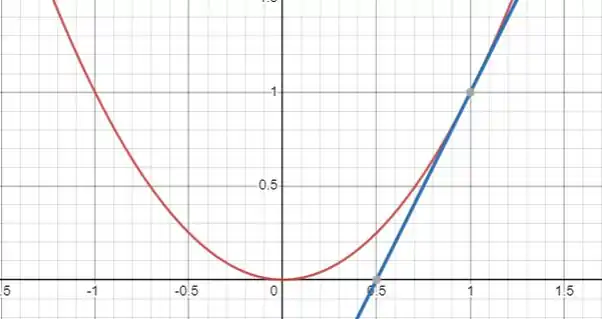
E o ponto onde elas se interceptam é quando elas são iguais, ou seja:
Assim temos que x varia de 0 até 1. MAAAS antes disso ele vai até 0.5, certo? Que é a interseção da reta com o eixo x. Desse modo, temos que dividir a região delimitada em duas partes, uma da parábola até o ponto ½, e depois da parábola com a reta até o ponto 1. Vamos lá?
Passo 3
A integral então é: