Use o método das cascas cilíndricas para encontrar o volume da região gerada pela rotação em torno do eixo x da região delimitada pelas curvas abaixo:
b)
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
Se liga só, as funções que temos que plotar num gráfico, obtemos:
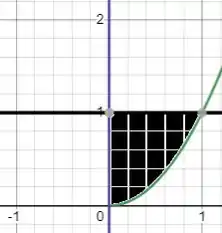
E é sobre essa região que vamos rotacionar e integrar para achar o volume.
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
O método das cascas cilíndricas é da seguinte forma:
Podemos ver que a função que depende g(y) cresce de 0 até .
Passo 3
assim:
É isso, carinha. Obrigado por ter vindo até aqui
