Ache o núumero b tal que a reta divida a região delimitada pelas curvas e em duas regiões de áreas iguais.
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão.
Nesse exercício temos uma região no plano cartesiano que é delimitada por uma parábola e por uma reta . Daí, queremos dividir essa região em duas partes iguais. Para isso, vamos traçar uma reta horizontal em .
Fazendo um gráfico das funções, temos:
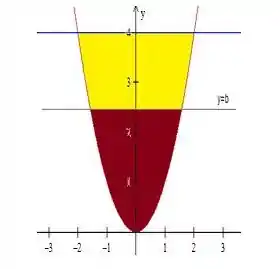
O nosso objetivo é calcular de modo que a área marrom ) e a amarela ) sejam iguais. Pegou a ideia? Beleza...
Mas, como podemos fazer isso?
Ou seja y varia de -2 a 2:
Bora pro próximo passo?
Passo 2
Obrigado por vir
Para pegarmos a parte da integração, devemos trocar a variável de integração, ou seja:
Assim podemos tomar a integral.
Concorda comigo que se fizemos a integral até b, e b até 4 e igualarmos, estamos fazendo com que ambas as integrais sejam iguais, certo? Ou seja, a área entre ambas é igual, concorda?! Fica mais fácil vendo. Então veja comigo.
Passo 3
Chamemos a integral marrom de e a amarela .
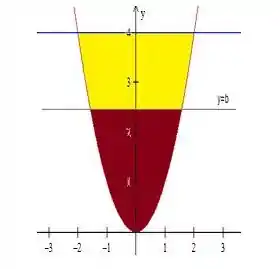
Assim:
Substituindo os limites de integração, temos:
Isolando , vem: