Lista 8 – Sem campus – Calculo – Funções de uma variável – Lista FUV-MADMAT – questão 2 item h
Esboce a região delimitada pelas curvas e decida se a integração deve ser feito com relação a variável x ou y. Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área de integração.
h)
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão
Seguinte... Temos, das funções dadas, o seguinte gráfico.
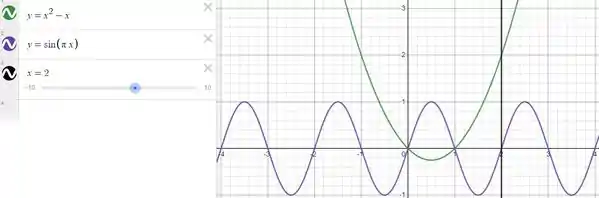
Bom... Visivelmente é mais fácil para nós fazermos a integração sobre a variável x. Mas a integral deverá ser tomada em dois passos, ou seja, para a região acima do eixo x e abaixo do eixo x.
Bora pro próximo passo?
Passo 2
Obrigado por vir
Os dois passos são:
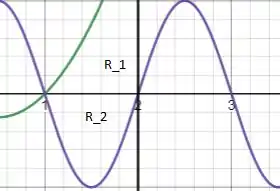
Para a primeira região, a integração é regida pela função verde, que de acordo com a primeira imagem, é a parábola. E o limite de integração em x é, de acordo, com a imagem, de [1,2]. Assim:
E para a outra parte:
Vemos que R_2 é regida pela função em roxo, mostrada na primeira imagem. E os limites de integração são os mesmos de R_1. Assim:
Façamos e para , e para . Logo:
Passo 3
Assim a área é:
Resposta
A região está no passo 1
A variável de integração é x.
E a área é: