Lista 8 – Sem campus – Calculo – Funções de uma variável – Lista FUV-MADMAT – questão 7 t item a
Determine o volume dos sólidos S, usando integração.
- Um cone circular reto de altura h e base r
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão
A imagem sobre a qual queremos o volume é:
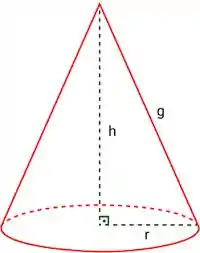
Sabemos que a formula para encontrarmos o volume é:
Também sabemos que:
Onde temos que encontrar alguma função de r que esteja em função de x. Vamos lá?!
Bora pro próximo passo?
Passo 2
Obrigado por vir.
Podemos fazer:
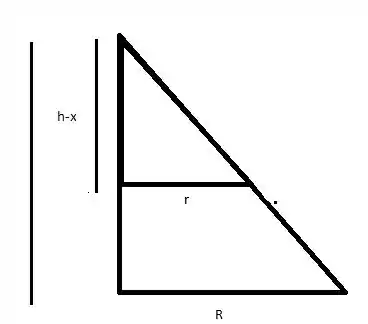
Onde:
Assim:
Passo 3
Assim, temos x varia de 0 até h. Logo:
Onde R é r da base dado, só trocarmos para que facilitasse o entendimento da explicação.
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d