Lista 8 – Sem campus – Calculo – Funções de uma variável – Lista FUV-MADMAT – questão 7 item e
Determine o volume dos sólidos S, usando integração.
e) a região delimitada por dois cilindros circulares retos que se interceptam perpendicularmente.
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão
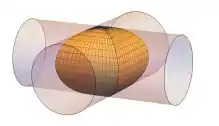
A forma de interceptação de dois cilindros nos dá uma imagem desse tipo:
E a interseção de ambos nos da o volume do tipo:
E veja que a imagem é simétrica, logo se achar o volume de um lado podemos multiplicar por 4 e acharemos o volume total.
Bora pro próximo passo?
Passo 2
Obrigado por vir
Fazendo um esboço, temos:
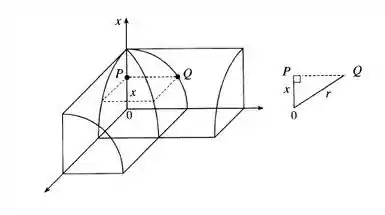
Esta é um quarto, conforme o que tínhamos dito no passo anterior, assim achando o volume desta parte e multiplicando por 4 poderemos achar o volume total da interseção dos cilindros!!
Passo 3
Sabemos que o volume é dado por:
E
E pela figura x varia de –r até +r.
Passo 4
Assim:
O 4 vem da multiplicação para o volume total, como dizemos antes.