Lista 8 – Sem campus – Calculo – Funções de uma variável – Lista FUV-MADMAT – questão 7 item c
Determine o volume dos sólidos S, usando integração.
c) uma calota esférica
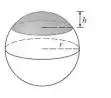
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão
Antes, tomemos considerações.
- dado que h é a altura da distancia do inicio da calota até o fim, façamos R a posição final do fim da calota.
Contando somente o inicio da calota em c, e o fim dela e R. Temos:
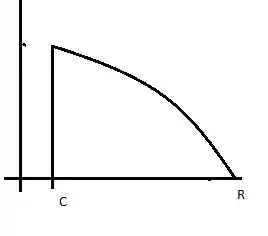
Bora pro próximo passo?
Passo 2
Obrigado por vir
Embora seja esférico e tome dimensão 3, o exemplo de uma calota é similar ao de um sólido de revolução, do tipo:
O volume esférico era no plano z=0, então
E como dito, y varia de c até R
Passo 3
Assim:
Onde c e R são definidos. De acordo com o desenho dado
Resposta
Onde c e R são definidos. De acordo com o desenho dado
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d