UFABC; Cálculo 1; Lista 9 – Funções de Uma Varável – Aplicações de Integração; Exercício 2e
2) Esboce a região delimitada pelas curvas e decida se a integração deve ser feita com relação a variável ou . Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área da região.
e)
Passo 1
Olá, pessoal! Tudo bem com vocês? Estou muito animada para responder essa questão. Então vamos nessa?
Esse é um exercício clássico de cálculo de área, uma das aplicações mais importantes da integração de funções. E como o objetivo é o cálculo da área, vamos aplicar nossas curvas em um gráfico para que possamos entender qual a área que deve ser calculada.
Inserindo no gráfico:
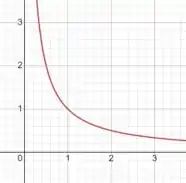
Agora, vamos inserir no gráfico:
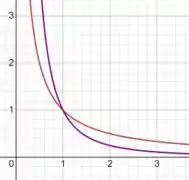
Por fim, vamos colocar no gráfico:
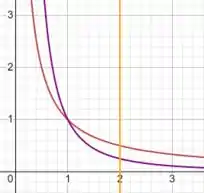
Perfeito! Mas e agora, qual o próximo passo? Vamos trabalhar melhor nisso...
Passo 2
Você viu que legal o motivo de termos no gráfico? Isso mesmo, ele é um dos limites da nossa integração!
Portanto só precisamos encontrar o outro limite e, para isso, vamos igualar as funções:
Portanto, o intervalo da nossa integração será entre os pontos e .
Bacana, né?
Ou seja, a área que queremos calcular é a área cinza, onde e é o intervalo da nossa integração:
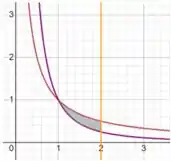
Como tanto as curvas quanto o intervalo de integração estão em função de , nossa integral deve ser com a variável .
Matematicamente, o que precisamos fazer, é integrar a diferença entre e no intervalo de a :
Passo 3
A partir de agora, vamos calcular a integral definida!
Como há a subtração dentro da integral:
E agora podemos integrar:
Passo 4
Como essa integral é definida, vamos aplicar o intervalo:
Simplificando:
Calculando:
Muito legal, né?
Pra essa questão é isso pessoal! Bora pra mais uma?