Lista de exercícios 9 – UFABC - Funções de uma variavel– questão 11
Deduza a fórmula do volume do toro obtido ao giramos o circulo em torno do eixo x
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
O gráfico da função f(x) é dado por:
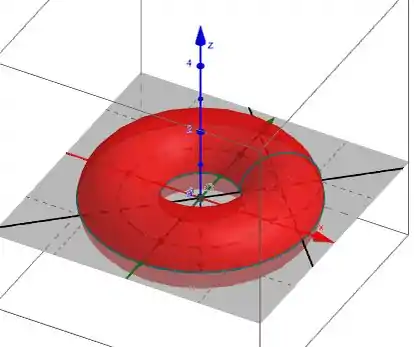
Que é dado por:
E é sobre essa função que vamos analisar e integrar
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Sendo assim, a função é limitada superiormente por e inferiormente por
Passo 3
Ao girarmos em torno do eixo x, deduzimos a formula do volume gerado por uma rotação, que é dado por:
Assim, pela definição de integrais, sabemos que a integral é dado pela área da função delimitada superior pela inferior, assim:
Pela imagem também podemos obter que
Passo 4
Assim, o volume do toro é dado por:
Para facilitar, façamos , logo:
De forma que:
Logo:
Portanto:
Façamos, agora sim, uma substituição real, então seja de forma que , quando e para ,
Assim ficando:
Veja como essa equação ficou fácil, baby. Assim:
Sabemos que
Assim:
É isso, carinha. Obrigado por ter vindo até aqui
