UFABC; Cálculo 1; Lista 9 – Funções de Uma Varável – Aplicações de Integração; Exercício 1b
1) Determine a área da região em cinza.
b)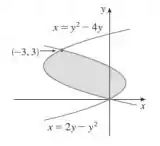 
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!
Esse é um exercício clássico de cálculo de área, uma das aplicações mais importantes da integração de funções. E como o objetivo é o cálculo da área, podemos analisar o seguinte:
Antes de tudo, você já deve ter reparado que as funções estão em , ou seja, a variação de é quem define . É o contrário do que estamos normalmente acostumados. Legal, mas o que isso muda no nosso exercício?
O que muda é que realizaremos as integrais de ao invés de . É como se estivéssemos olhando o gráfico dessa maneira:
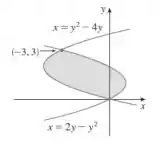
A partir de agora, podemos voltar para o conceito normal de área por integral:
Quando realizamos a integração de uma função qualquer entre os pontos definidos e , encontramos a sua área.
Então, se integramos a curva (que chamaremos de a partir de agora) entre os pontos e , obteremos a seguinte área hachurada:
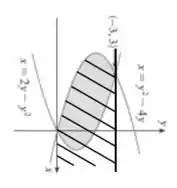
Vamos chamar essa área de .
Da mesma forma, se integrarmos a curva (que chamaremos de a partir de agora) entre os pontos e , obteremos a seguinte área hachurada:
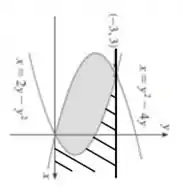
Vamos chamar essa área de .
Como queremos encontrar a área pintada de cinza, com certeza você já percebeu que é só subtrair de .
Matematicamente, o que precisamos fazer então, é integrar a diferença entre e no intervalo de a :
Passo 2
A partir de agora, vamos calcular a integral definida!
Podemos simplificar para:
Como há a subtração dentro da integral:
E como temos constantes multiplicando as funções:
E agora podemos integrar:
Simplificando:
Passo 3
Como essa integral é definida, vamos aplicar o intervalo:
Calculando:
Ufa! Terminamos!
Pra essa questão é isso pessoal! Bora pra mais uma?