Lista de exercícios 9 – UFABC - Funções de uma variavel– questão 10 item a
Encontre o volume do sólido que permanece depois que um furo circular de um raio é perfurado através do centro de um esfera sólida de raio por:
- Seções transversais
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
Se liga só, fazendo um esboço da esfera e do cilindro dentro dela, temos:
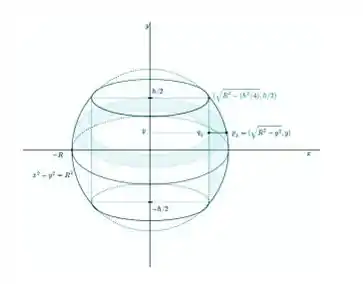
Que já nos dá os valores que determinam os limites
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Sabemos que o volume é dado por:
E no caso da área de uma seção circular de uma esfera, sabemos que é
E por fim, saca só, a seção é tem o tipo de função , assim . Assim essa é a equação pra esfera.
Mas calma já, jovem mancebo, falta ainda o cilindro interno. O cilindro tem por equação , mas pela imagem, temos que , logo . Assim já temos tudo.
Passo 3
Esse desenho foi brabo né? Nele também obtemos os limites pra y, isso é
Saco só, como queremos saber o volume que resta, então podemos fazer o volume da esfera menos o volume do cilindro, certo?! Assim:
É isso, carinha. Obrigado por ter vindo até aqui
