Lista 8 – Sem campus – Calculo – Funções de uma variável – Lista FUV-MADMAT – questão 7 item b
Determine o volume dos sólidos S, usando integração.
b) um cone truncado de base circular.
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão
Um cone truncado é um cone cortado, de forma que parece um tronco do cone.
Se queremos achar o volume de algo, podemos fazer:
E área do cone é:
Agora só devemos achar uma função que dependa de x para integrarmos, Bora lá?!
Bora pro próximo passo?
Passo 2
Obrigado por vir
Fazendo uma função para:
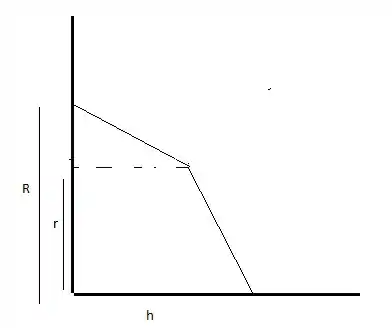
Onde temos que:
Ou seja, para x=0, y=R, e h=r, y=r e assim os demais.
Assim tomando o produtos:
Onde essa função y é .
Passo 3
Sabemos que x compreende de 0 até h. Logo:
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d